Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, có đồ thị li độ theo thời gian như hình vẽ.
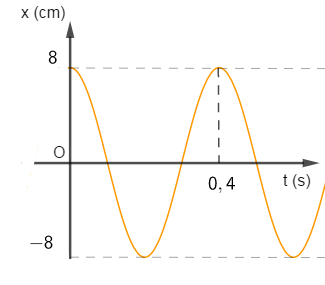
Lấy \(g = {\pi ^2} = 10m/{s^2}\). Khoảng thời gian ngắn nhất giữa hai lần công suất tức thời của lực đàn hồi bằng 0 là:
Trả lời bởi giáo viên
+ Từ đồ thị, ta có:
- Biên đọ dao động: \(A = 8cm\)
- Chu kì dao động: \(T = 0,4s\)
Chọn chiều dương hướng xuống, ta có:
+ Độ dãn của lò xo tại vị trí cân bằng: \(\Delta l = \dfrac{{mg}}{k} = \dfrac{{mg}}{{m{\omega ^2}}} = \dfrac{g}{{{{\left( {\dfrac{{2\pi }}{T}} \right)}^2}}} = \dfrac{{10}}{{{{\left( {\dfrac{{2\pi }}{{0,4}}} \right)}^2}}} = 0,04m = 4cm\)
+ Lực đàn hồi tại vị trí bất kì:
+ Công suất tức thời: \(P = \left| {Fv} \right| = k\left| {(\Delta l + x)v} \right|\)
Ta có: P = 0 khi \(\left[ \begin{array}{l}x = - \Delta l = - 4cm\\v = 0 \to x = \pm A\end{array} \right.\)
Vẽ vòng tròn lượng giác, ta được:
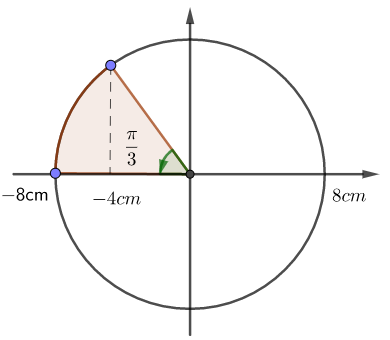
=> Khoảng thời gian ngắn nhất giữa hai lần công suất tức thời của lực đàn hồi bằng 0 chính bằng khoảng thời gian đi từ \( - 4cm\) đến \( - 8cm\) hoặc ngược lại.
Ta có: \(\Delta \varphi = \omega \Delta t\)
=> Khoảng thời gian đó là: \(\Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{\pi }{3}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{T}{6} = \dfrac{{0,4}}{6} = \dfrac{1}{{15}}s\)
Hướng dẫn giải:
+ Đọc đồ thị li độ theo thời gian
+ Áp dụng biểu thức tính độ dãn tại vị trí cân bằng của con lắc lò xo treo thẳng đứng: \(\Delta l = \dfrac{{mg}}{k}\)
+ Áp dụng biểu thức tính lực đàn hồi:
+ Áp dụng biểu thức tính công suất tức thời: \(P = \left| {Fv} \right|\)
+ Sử dụng vòng tròn lượng giác và biểu thức \(\Delta \varphi = \omega \Delta t\)

