Một chất điểm M chuyển động với tốc độ 0,75 m/s trên đường tròn có đường kính bằng 0,5 m. Hình chiếu M’ của điểm M lên đường kính của đường tròn dao động điều hoà. Tại thời điểm t = 0 s, M’ đi qua vị trí cân bằng theo chiều âm. Khi t = 8 s, hình chiếu M’ qua li độ
Trả lời bởi giáo viên
Tần số góc của dao động:
\(\omega = \frac{{{v_{\max }}}}{A} = \frac{{0,75}}{{0,25}} = 3\,\,\left( {rad/s} \right)\)
Tại thời điểm t = 8 s, vật quay được góc:
\(\Delta \varphi = \omega .\Delta t = 3.8 = 24\,\,\left( {rad} \right) = 7,639\pi = 6\pi + 1,639\pi \)
Biểu diễn trên VTLG, ta có:
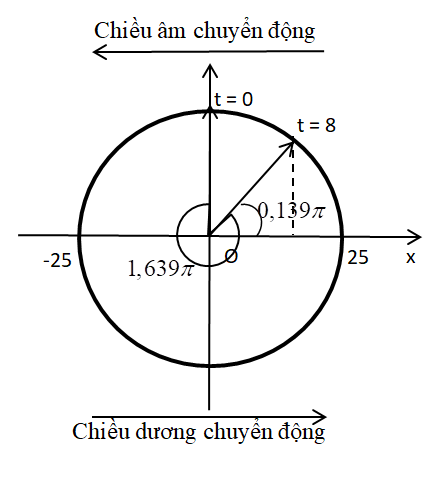
Từ VTLG, ta thấy tại thời điểm t = 8 s, vật chuyển động theo chiều âm và ở vị trí:
\(x = A.cos0,139\pi = 0,25.cos0,139\pi = 0,2264\,\,\left( m \right) = 22,64\,\,\left( {cm} \right)\)
Hướng dẫn giải:
Sử dụng vòng tròn lượng giác và các công thức \(\Delta \varphi = \omega .\Delta t\); công thức tốc độ lớn nhất của chất điểm dao động \({v_{\max }} = A.\omega \)