Câu hỏi:
2 năm trước
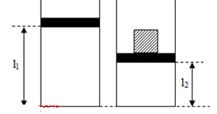
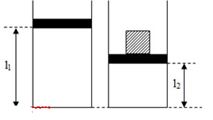
Một bình thủy tinh hình trụ tiết diện \(100c{m^2}\) chứa khí lí tưởng bị chặn với tấm chắn có khối lượng không đáng kể, áp suất, nhiệt độ, chiều cao của cột không khí bên trong bình lần lượt là \(76cmHg\), \({20^0}C\) và \(60cm\). Đặt lên tấm chắn vật có trọng lượng \(408N\), cột khí bên trong bình có chiều cao \(50cm\). Nhiệt độ của khí bên trong bình là:
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
- Trạng thái 1: \(\left\{ \begin{array}{l}{T_1} = 20 + 273 = 293K\\{p_1} = 1,{013.10^5}Pa\\{V_1} = {l_1}S\end{array} \right.\)
- Trạng thái 2: \(\left\{ \begin{array}{l}{T_2} = ?\\{p_2} = {p_1} + \frac{F}{S} = 1,{013.10^5} + \frac{{408}}{{{{100.10}^{ - 4}}}} = 1,{421.10^5}Pa\\{V_2} = {l_2}S\end{array} \right.\)
Áp dụng phương trình trạng thái của khí lý tưởng, ta có:
\(\begin{array}{l}\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \leftrightarrow \frac{{{p_1}.{l_1}S}}{{{T_1}}} = \frac{{{p_2}.{l_2}S}}{{{T_2}}}\\{T_2} = \frac{{{p_2}{l_2}{T_1}}}{{{p_1}{l_1}}} = \frac{{1,{{421.10}^5}.50.293}}{{1,{{013.10}^5}.60}} = 342,5K\end{array}\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính nhiệt độ tuyệt đối: \(T = t + 273\)
+ Vận dụng biểu thức tính thể tích: \(V = l{\rm{S}}\)
+ Vận dụng phương trình trạng thái của khí lý tưởng: \(\frac{{pV}}{T} = const\)
Câu hỏi khác
- Bài tập thuyết động học phân tử chất khí lý 10 có lời giải
- Bài tập định luật sác-lơ. đường đẳng tích lý 10 có lời giải
- Bài tập định luật bôilơ - mariốt. Đường đẳng nhiệt lý 10 có lời giải
- Bài tập định luật gay - luy - sác. đường đẳng áp lý 10 có lời giải
- Bài tập phương trình trạng thái của khí lí tưởng lý 10 có lời giải
