Câu hỏi:
2 năm trước
Hình thang \(ABCD \,(AB // CD)\) có \(AB = 9cm, CD = 12cm\), hai đường chéo cắt nhau tại \(O\).
Chọn khẳng định không đúng.
Trả lời bởi giáo viên
Đáp án đúng: a
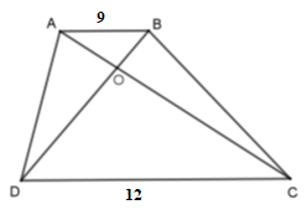
\(AB{\rm{//}}CD\) nên \(\Delta AOB\backsim\Delta COD.\)
Tỉ số đồng dạng \(\dfrac{{AO}}{{OC}} = \dfrac{{BO}}{{OD}} = \dfrac{{AB}}{{CD}} = \dfrac{9}{{12}} = \dfrac{3}{4}\) nên B, C đúng.
Lại có: \(AB//CD\) nên \(\widehat {ABD} = \widehat {BDC}\) (so le trong) nên D đúng.
Đáp án A sai vì viết sai thứ tự các đỉnh của hai tam giác đồng dạng.
Hướng dẫn giải:
Sử dụng định lý về tam giác đồng dạng và tỉ số đồng dạng.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
