Hai vật A và B có cùng khối lượng \(1kg\) và có kích thước nhỏ được nối với nhau bằng một sợi dây mảnh nhẹ dài \(15cm\), hai vật được treo vào lò xo có độ cứng \(k{\rm{ }} = 100{\rm{ }}N/m\) tại nơi có gia tốc trọng trường \(g = 10{\rm{ }}m/{s^2}\), lấy \({\pi ^2} = 10\). Khi hệ vật và lò xo đang ở vị trí cân bằng đủ cao so với mặt đất, người ta đốt sợi dây nối hai vật và vật B sẽ rơi tự do còn vật A sẽ dao động điều hòa theo phương thẳng đứng. Lần đầu tiên vật A lên đến vị trí cao nhất thì khoảng cách giữa hai vật bằng:
Trả lời bởi giáo viên
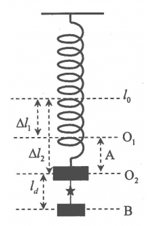
Tại vị trí cân bằng:
+ Khi chỉ có vật A thì lò xo dãn: \(\Delta {l_1} = \frac{{{m_A}g}}{k} = 10cm\)
+ Khi treo đồng A và B thì lò xo dãn: \(\Delta {l_2} = \frac{{({m_A} + {m_B})g}}{k} = 20cm\)
Khi hệ vật đang ở VTCB, dây đứt, vật A dao động điều hòa với biên độ \(A = \Delta {l_2} - \Delta {l_1} = 20 - 10 = 10cm\)
+ Chu kỳ con lắc lò xo khi gắn vật A là: \(T = 2\pi \sqrt {\frac{{\Delta {l_1}}}{g}} = 2\pi \sqrt {\frac{{0,1}}{{10}}} = \frac{\pi }{5}s\)
Thời gian vật A đi từ vị trí đốt dây (biên dưới) đến vị trí cao nhất lần đầu tiên (biên trên ) hết \(t = \frac{T}{2} = \frac{\pi }{{10}}s\) khi đó, vị trí của vật A là : \({x_A} = - 10cm\)
+ Sau khi đót dây nối hai vật, vật B rơi tự do từ B cách O1:
\({O_1}B = B{O_2} + {O_1}{O_2} = {l_d} + A = 15 + 10 = 25cm\)
+ Tọa độ của B: \({x_B} = {\rm{ }}{O_1}B{\rm{ }} + {\rm{ }}\frac{{g{t^2}}}{2} = 0,25 + \frac{{10.{{\left( {\frac{\pi }{{10}}} \right)}^2}}}{2} = 0,75m = 75cm\)
Vậy khoảng cách giữa hai vật lúc này là: \(\Delta x = {x_B} - {x_A} = 75 - ( - 10) = 85cm\)

