Hai nguồn s1 và s2 cách nhau 4cm dao động với pt u1 = 6cos(100πt + 5π/6)(mm) và
u2 = 8cos(100πt + π/6) (mm) với λ = 2cm Gọi P,Q là hai điểm trên mặt nước sao cho tứ giác S1S2PQ là hình thang cân có diện tích 12cm2 và PQ = 2cm là một đáy của hình thang. Tìm số điểm dao động với biên độ \(2\sqrt {13} mm\) trên S1P.
Trả lời bởi giáo viên
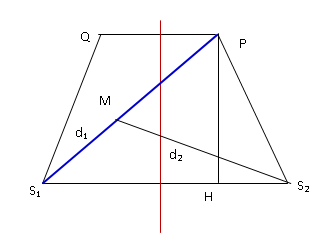
Xét điểm M trên S1P
S1M = d1; S2M = d2.
Theo bài S1S2PQ là hình thang cân, PQ = 2cm, S1S2 = 4cm
Ta có:
\({S_{{S_1}{S_2}PQ}} = \frac{1}{2}\left( {PQ + {S_1}{S_2}} \right)PH = 12 \leftrightarrow \frac{1}{2}\left( {2 + 4} \right)PH = 12 \to PH = 4cm\)\(\begin{array}{l}{S_1}{P_{}} = \sqrt {P{H^2} + {S_1}{H^2}} = \sqrt {{4^2} + {3^2}} = 5cm\\{S_2}{P_{}} = \sqrt {P{H^2} + {S_2}{H^2}} = \sqrt {{4^2} + {1^2}} = \sqrt {17} cm\end{array}\)
Sóng từ S1 và S2 truyền đến M:
\(\begin{gathered}{u_{1M}} = 6cos(100\pi t + \frac{{5\pi }}{6} - \frac{{2\pi {d_1}}}{\lambda }) = 6cos(100\pi t + \frac{{5\pi }}{6} - \pi {d_1}) \hfill \\{u_{2M}} = 8cos(100\pi t + \frac{\pi }{6} - \frac{{2\pi {d_2}}}{\lambda }) = 8cos(100\pi t + \frac{\pi }{6} - \pi {d_2}) \hfill \\\end{gathered} \)
Sóng tổng hợp tại M:
\({u_M} = 6cos(100\pi t + \frac{{5\pi }}{6} - {\text{ }}\pi {d_1}){\text{ }} + {\text{ }}8cos(100\pi t + \frac{\pi }{6} - \pi {d_2}) = Acos(100\pi t + \varphi )\)
Với \({A^2} = {A_1}^2 + {\text{ }}{A_2}^2 + 2{A_1}{A_2}cos(\frac{{2\pi }}{3} + \pi \left( {{d_2}-{d_1}} \right))\)
\(\begin{gathered}\Rightarrow {\text{ }}cos(\frac{{2\pi }}{3} + {\text{ }}\pi \left( {{d_2}-{\text{ }}{d_1}} \right)){\text{ }} = \frac{{{A^2} - A_1^2 - A_2^2}}{{2{A_1}{A_2}}} = \frac{{52 - 36 - 64}}{{2.6.8}} = - 0,5 \hfill \\\Rightarrow \frac{{2\pi }}{3} + {\text{ }}\pi \left( {{d_2}-{\text{ }}{d_1}} \right) = \pm \frac{{2\pi }}{3} + k2\pi \hfill \\\\ \\\end{gathered} \)
\( \Rightarrow \left[ \begin{array}{l}{d_2} - {d_1} = 2k\\{d_2} - {d_1} = 2k - \frac{4}{3}\end{array} \right.\)
Mặt khác :
\(\sqrt {17} -{\rm{ }}5{\rm{ }} < {\rm{ }}{d_2}-{\rm{ }}{d_1} < {\rm{ }}4\)
Khi
\(\sqrt {17} -{\rm{ }}5{\rm{ }} < {\rm{ }}{d_2}-{\rm{ }}{d_1} = {\rm{ }}2k{\rm{ }} < {\rm{ }}4\) => Có 2 giá trị của k: k1 = 0; k2 = 1
Khi
Khi:
\(\sqrt {17} - 5 < {d_2} - {d_1} = 2k - \frac{4}{3} < 4\)
=> Có 2 giá trị của k: k’1 = 1; k’2 = 2
Như vậy trên S1P có 4 điểm dao động với biên độ \(2\sqrt {13} cm\)
Hướng dẫn giải:
+ Sử dụng công thức tính diện tích hình thang: S = 1/2 (đáy lớn + đáy nhỏ).chiều cao
+ Viết phương trình sóng tại một điểm bất kì trên S1P
+ Áp dụng công thức tính biên độ dao động tổng hợp: \({A^2} = {A_1}^2 + {A_2}^2 + 2{A_1}{A_2}\cos \Delta \varphi \)

