Gọi S là tập hợp tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số \(y = \left| {\dfrac{1}{4}{x^4} - 14{x^2} + 48x + m - 30} \right|\) trên đoạn \(\left[ {0;2} \right]\) không vượt quá 30. Tổng giá trị của phần tử tập hợp S bằng bao nhiêu ?

Xét hàm số \(f\left( x \right) = \dfrac{1}{4}{x^4} - 14{x^2} + 48x + m - 30\) có \(y' = {x^3} - 28x + 48\).

\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 6\\x = 4\\x = 2\end{array} \right.\)

Bảng biến thiên của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {0;2} \right]\):

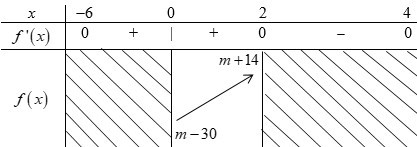
TH1: \(m - 30 \ge 0\) \( \Leftrightarrow m \ge 30\).

\( \Rightarrow \mathop {\max }\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = m + 14 \le 30 \Leftrightarrow m \le 16\) (Vô lí).

TH2: \(m - 30 < 0 \le m + 14\) \( \Leftrightarrow  - 14 \le m < 30\).

+ Nếu \(m + 14 \ge 30 - m \Leftrightarrow m \ge 8\), kết hợp điều kiện ta có: \(8 \le m < 30\) thì \(\mathop {\max }\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = m + 14 \le 30 \Leftrightarrow m \le 16\).

\( \Rightarrow 8 \le m \le 16\).

+ Nếu \(m + 14 < 30 - m \Leftrightarrow m < 8\), kết hợp điều kiện ra có \( - 14 \le m < 8\) thì \(\mathop {\max }\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = 30 - m \le 30 \Leftrightarrow m \ge 0\).

\( \Rightarrow 0 \le m < 8\)

Vậy trường hợp 2 ta có \(0 \le m \le 16\) thỏa mãn.

TH3: \(m + 14 < 0 \Leftrightarrow m <  - 14\).

\( \Rightarrow \mathop {\max }\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = 30 - m \le 30 \Leftrightarrow m \ge 0\)  (vô lí).

Từ các trường hợp \( \Rightarrow m \in \left[ {0;16} \right]\).

\( \Rightarrow S = \left\{ {0;1;2;3;...;16} \right\}\).

Vậy tổng các phần tử của \(S\) bằng \(0 + 1 + 2 + ... + 16 = \dfrac{{16.17}}{2} = 136\).