Câu hỏi:
2 năm trước
Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của một hình vuông. Tỉ số $\dfrac{R}{r}$ là:
Trả lời bởi giáo viên
Đáp án đúng: d
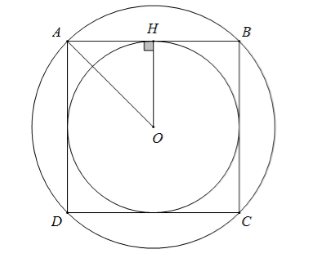
Giả sử hình vuông ABCD nội tiếp đường tròn (O)
⇒ O cũng là tâm đường tròn nội tiếp hình vuông
Gọi H là trung điểm AB ⇒ OH ⊥ AB tại H
Ta có R = OA, r = OH
Vì AO là phân giác của góc BAD nên
$\widehat {HAO} = \dfrac{{\widehat {BAD}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ $
Xét tam giác AHO vuông tại H có $ \sin \widehat {HAO} = \dfrac{{OH}}{{OA}}$$ \Leftrightarrow \dfrac{{OH}}{{OA}} = \sin {45^0} = \dfrac{1}{{\sqrt 2 }} $$\Leftrightarrow \dfrac{{OA}}{{OH}} = \sqrt 2 $ hay \(\dfrac{R}{r} = \sqrt 2 .\)
Hướng dẫn giải:
Chứng minh bán kính đường tròn ngoại tiếp và nội tiếp hình vuông là cạnh huyền và cạnh góc vuông của một tam giác vuông cân, từ đó suy ra tỉ lệ
