Gọi $a$ là số thực lớn nhất để bất phương trình ${x^2} - x + 2 + a\ln \left( {{x^2} - x + 1} \right) \ge 0$ nghiệm đúng với mọi $x \in R.$ Mệnh đề nào sau đây đúng?

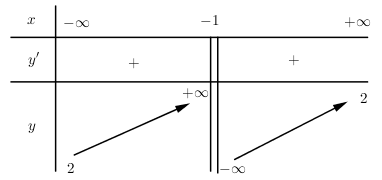
Đặt $t = {x^2} - x + 1 = {\left( {x - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \ge \dfrac{3}{4}$

Khi đó BPT trở thành $f\left( t \right) = t + 1 + a\ln t \ge 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {t \in \left[ {\dfrac{3}{4}; + \infty {\rm{\;}}} \right)} \right)$

Ta có: $f'\left( t \right) = 1 + \dfrac{a}{t} = 0 \Leftrightarrow t =  - a.$

Mặt khác $\mathop {\lim }\limits_{t \to  + \infty } {\mkern 1mu} f\left( t \right) =  + \infty ;f\left( {\dfrac{3}{4}} \right) = \dfrac{7}{4} + a\ln \dfrac{3}{4}$

Với $a > 0 \Rightarrow f\left( t \right)$ đồng biến trên $\left[ {\dfrac{3}{4}; + \infty {\rm{\;}}} \right) \Rightarrow f\left( t \right) \ge 0\;\left( {\forall t \in \left[ {\dfrac{3}{4}; + \infty {\rm{\;}}} \right)} \right) \Leftrightarrow \mathop {Min}\limits_{\left[ {\dfrac{3}{4}; + \infty {\rm{\;}}} \right)} {\mkern 1mu} f\left( t \right) = \dfrac{7}{4} + a\ln \dfrac{3}{4} \ge 0$

$ \Leftrightarrow a\ln \dfrac{3}{4} \ge \dfrac{{ - 7}}{4} \Leftrightarrow a \le \dfrac{{\dfrac{{ - 7}}{4}}}{{\ln \dfrac{3}{4}}} \approx 6,08$. Vì đề bài yêu cầu tìm số thực lớn nhất nên suy ra $a \in \left( {6;7} \right].$