Góc chiết quang của lăng kính bằng A = 60. Chiếu một tia sáng trắng vào mặt bên của lăng kính theo phương vuông góc với mặt phẳng phân giác của góc chiết quang. Đặt một màn quan sát, sau lăng kính, song song với mặt phẳng phân giác của góc chiết quang của lăng kính và cách mặt này 2m. Chiết suất của lăng kính đối với tia đỏ là nd = 1,5 và đối với tia tím là nt = 1,56 . Độ rộng của quang phổ liên tục trên màn quan sát bằng
Trả lời bởi giáo viên
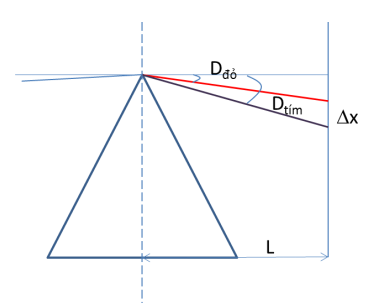
Ta có:
\({{\mathop{\rm tanD}\nolimits} _d} = \frac{{{x_d}}}{L},{\rm{ }}{{\mathop{\rm tanD}\nolimits} _t} = \frac{{{x_t}}}{L}\)
Vì A≪ \( \to \left\{ \begin{array}{l}{D_d} \ll \\{D_t} \ll \end{array} \right. \to {\mathop{\rm tanD}\nolimits} \approx sinD \approx D\)
\(\begin{array}{l}\Delta x = {x_t} - {{\rm{x}}_d} = ({n_t} - 1)AL - ({n_d} - 1)AL\\ = ({n_t} - {n_d})LA = (1,56 - 1,5)2.\frac{{6\pi }}{{180}} = 0,01257m = 12,57mm\end{array}\)
Hướng dẫn giải:
Áp dụng công thức tính bề rộng quang phổ:
\(\Delta x = {x_t} - {x_d} = \left( {{n_t} - {n_d}} \right)LA\)
Giải thích thêm:
Đổi độ sang rad

