Câu hỏi:
2 năm trước
Đường tròn tâm \(I\) nội tiếp tam giác \(ABC\) tiếp xúc với \(BC,AB,AC\) lần lượt ở \(D,E,F\). Đường thẳng qua \(E\) song song với \(BC\) cắt \(AD,DF\) lần lượt ở \(M,N\). Khi đó \(M\) là trung điểm của đoạn thẳng
Trả lời bởi giáo viên
Đáp án đúng: a
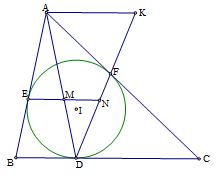
+ Vì đường tròn \((I)\) tiếp xúc với các cạnh tại \(D,E,F\) nên suy ra \(AE = AF,BE = BD,CD = CF\).
+ Dựng \(AK//BD\left( {K \in DF} \right)\) ta có: \(\dfrac{{MN}}{{AK}} = \dfrac{{MD}}{{DA}}\), \(\dfrac{{EM}}{{BD}} = \dfrac{{AM}}{{AD}}\).
Ta cần chứng minh: \(\dfrac{{MD}}{{DA}}.AK = \dfrac{{AM}}{{AD}}.BD \Leftrightarrow \dfrac{{MD}}{{AM}} = \dfrac{{BD}}{{AK}}\).
Nhưng \(AK = AF = AE\), \(BD = BE\) nên ta cần chứng minh: \(\dfrac{{MD}}{{AM}} = \dfrac{{BE}}{{AE}}\) (điều này là hiển nhiên theo định lý Ta-let).
Hướng dẫn giải:
+ Dựng \(AK//BD\left( {K \in DF} \right)\)
+ Sử dụng tính chất hai tiếp tuyến cắt nhau và định lý Ta-lét để chỉ ra vị trí điểm \(M.\)
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
