Câu hỏi:
2 năm trước
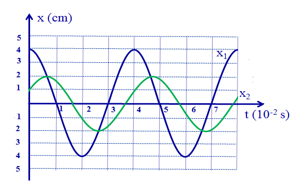
Đồ thị li độ theo thời gian của chất điểm 1 (đường x1) và chất điểm 2 (đường x2) như hình vẽ. Biết hai vật dao động trên hai đường thẳng song song cách nhau \(2cm\) với cùng một hệ trục toạ độ. Khoảng cách lớn nhất giữa hai vật (theo phương dao động) gần giá trị nào nhất:
Trả lời bởi giáo viên
Đáp án đúng: a
Từ đồ thị ta có được
- Hai dao động có cùng chu kì T
- Chất điểm 1:
+ \({A_1} = {\rm{ }}4cm\)
+ Tại t = 0 vật đang ở biên dương \( \Rightarrow {\varphi _1} = 0rad\)
- Chất điểm 2:
+ \({A_2} = 2cm\)
+ Tại t = 0 vật qua li độ x = 1cm theo chiều dương \( \Rightarrow {\varphi _2} = - \frac{\pi }{3}rad\)
- Phương trình dao động của hai dao động là:
\(\begin{array}{l}{x_1} = 4\cos (\omega t)cm\\{x_2} = 2\cos (\omega t - \frac{\pi }{3})cm\end{array}\)
- Khoảng cách của hai vật trong quá trình dao động: \(d = \sqrt {{2^2} + {{\left| {{x_1} - {x_2}} \right|}^2}} = \sqrt {{2^2} + {{\left( {\Delta {x_{\max }}\cos (\omega t + \varphi )} \right)}^2}} \)
Với \(\Delta {x_{max}}\) là khoảng cách lớn nhất giữa hai vật trong quá trình dao động
\(\Delta x = \left| {{x_1} - {x_2}} \right| = \left| {{x_1} + ( - {x_2})} \right|\)
\({x_2} = 2\cos (\omega t - \frac{\pi }{3})\)nên \( - {x_2} = - 2\cos (\omega t + \frac{\pi }{3}) = 2cos(\omega t - \frac{\pi }{3} + \pi ) = 2cos(\omega t + \frac{{2\pi }}{3})\)
Do đó
\(\begin{array}{l}\Delta {x_{\max }} = \sqrt {{A_1}^2 + {A_2}^2 + 2{A_1}{A_2}\cos (\Delta \varphi )} \\ = \sqrt {{4^2} + {2^2} + 2.2.4.cos\frac{{2\pi }}{3}} = 2\sqrt 3 cm\end{array}\)
Ta suy ra, khoảng cách lớn nhất: \({d_{max}} = \sqrt {{2^2} + \Delta x_{max}^2} = \sqrt {{2^2} + {{\left( {2\sqrt 3 } \right)}^2}} = 4cm\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
