Câu hỏi:
2 năm trước
Diện tích hình phẳng của phần tô đậm trong hình vẽ bên được tính theo công thức nào dưới đây?
Trả lời bởi giáo viên
Đáp án đúng: a
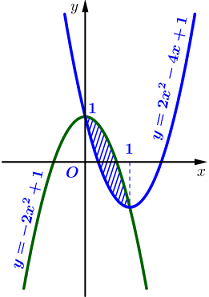
Dựa vào đồ thị hàm số ta thấy hoành độ giao điểm của hai đồ thị hàm số \(y = 2{x^2} - 4x + 1\) và \(y = - 2{x^2} + 1\) là \(x = 0\) và \(x = 1\).
Hình phẳng giới hạn bởi hai đồ thị hàm số \(y = 2{x^2} - 4x + 1\), \(y = - 2{x^2} + 1\), đường thẳng \(x = 0,\,\,x = 1\) là: \(S = \int\limits_0^1 {\left| {\left( {2{x^2} - 4x + 1} \right) - \left( { - 2{x^2} + 1} \right)} \right|dx} \).
Dựa vào đồ thị hàm số ta thấy trên đoạn \(\left[ {0;1} \right]\) thì đồ thị hàm số \(y = - 2{x^2} + 1\) nằm hoàn toàn phía trên đồ thị hàm số \(y = 2{x^2} - 4x + 1\), do đó \( - 2{x^2} + 1 > 2{x^2} - 4x + 1\,\,\forall x \in \left[ {0;1} \right]\).
\( \Rightarrow \left| {\left( {2{x^2} - 4x + 1} \right) - \left( { - 2{x^2} + 1} \right)} \right| = - 2{x^2} + 1 - 2{x^2} + 4x - 1 = - 4{x^2} + 4x\).
Vậy \(S = \int\limits_0^1 {\left( { - 4{x^2} + 4x} \right)dx} \).
Hướng dẫn giải:
- Xác định hoành độ giao điểm của hai đồ thị hàm số để suy ra hai cận.
- Diện tích hình phẳng giới hạn bởi đồ thi hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
- Dựa vào đồ thị hàm số để phá trị tuyệt đối.
Câu hỏi khác
- Bài tập nguyên hàm toán 12 có lời giải
- Bài tập tích phân các hàm số cơ bản toán 12 có lời giải
- Bài tập tích phân có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp từng phần để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp đổi biến để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
