Đề thi THPT QG 2022 – mã đề 124
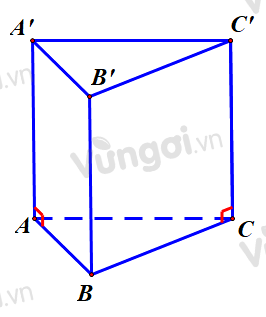
Cho hình lăng trụ đứng \(ABC.{A^\prime }{B^\prime }{C^\prime }\) có đáy $A B C$ là tam giác vuông tại \(B,AC = 2,AB = \sqrt 3 \) và \(A{A^\prime } = 1\) (tham khảo hình bên). Góc giữa hai mặt phẳng \(\left( {AB{C^\prime }} \right)\) và \((ABC)\) bằng
Trả lời bởi giáo viên
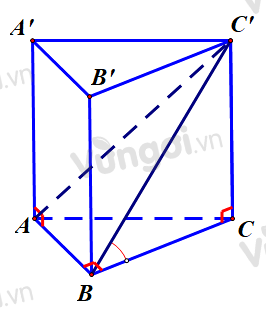
Ta có: \(CC' \bot \left( {ABC} \right)\)\( \Rightarrow BC\) là hình chiếu của \(BC'\) lên \(\left( {ABC} \right)\)
Do \(AB \bot BC \Rightarrow AB \bot BC'\)(Định lý 3 đường vuông góc)
\( \Rightarrow AB \bot \left( {BCC'} \right)\)
Mà \(\left( {BCC'} \right) \cap \left( {ABC} \right) = BC;\)\(\left( {BCC'} \right) \cap \left( {ABC'} \right) = BC'\)
=> Góc giữa hai mặt phẳng \(\left( {AB{C^\prime }} \right)\) và \((ABC)\) bằng góc giữa BC và BC’ và bằng \(\widehat {CBC'}\)
Ta có: \(BC = \sqrt {A{C^2} - A{B^2}} = 1;CC' = AA' = 1\) \( \Rightarrow \tan \widehat {CBC'} = 1 \Rightarrow \widehat {CBC'} = {45^o}\)
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng \(\left( {AB{C^\prime }} \right)\) và \((ABC)\)
- Tính góc.