Câu hỏi:
1 năm trước
Đề thi THPT QG 2022 – mã đề 124
Cho hình nón có góc ở đỉnh bằng \({120^o}\) và chiều cao bằng 1. Gọi \((S)\) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của \((S)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
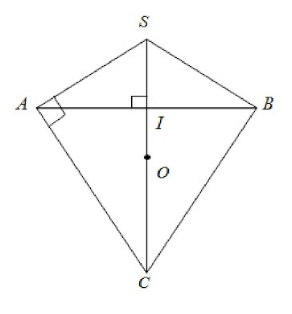
Giả sử thiết diện qua trục của hình nón là tam giác SAB với S là đỉnh hình nón và AB là đường kính đường tròn đáy.
Gọi $I$ là tâm đường tròn đáy.
\( \Rightarrow \widehat {ASB} = {120^0};SI = 1 \Rightarrow IB = \sqrt 3 \Rightarrow AB = 2\sqrt 3 \)
Mặt cầu chứa đường tròn đáy của hình nón thì tâm $O$ của mặt cầu thuộc đường thẳng vuông góc với mặt phẳng đáy $I$.
Mà SI luôn vuông góc với mặt phẳng đáy
=> S,O,I thẳng hàng.
=> O là điểm cách đều S, A và B
=> O là tâm đường tròn ngoại tiếp tam giác SAB.
Bán kính mặt cầu là \(R = OA = \dfrac{{AB}}{{2.\sin \widehat {ASB}}} = \dfrac{{2\sqrt 3 }}{{2.\dfrac{{\sqrt 3 }}{2}}} = 2\)
Khi đó diện tích mặt cầu là \({S_{cau}} = 4\pi {R^2} = 16\pi \)
Hướng dẫn giải:
- Giả sử thiết diện qua trục của hình nón là tam giác SAB với S là đỉnh hình nón và AB là đường kính đường tròn đáy.
- Gọi $I$ là tâm đường tròn đáy.
- Chứng tỏ tâm O của mặt cầu là tâm đường tròn ngoại tiếp tam giác SAB.
- Tính bán kính đường tròn ngoại tiếp.
Câu hỏi khác
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 101 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 102 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 103 có lời giải chi tiết
- Đề thi thpt qg chính thức - 2021 Toán12 - mã đề 104 có lời giải chi tiết
- Đề thi THPT QG chính thức - 2022 - mã đề 122 có lời giải chi tiết
