Đề thi THPT QG 2022 – mã đề 124

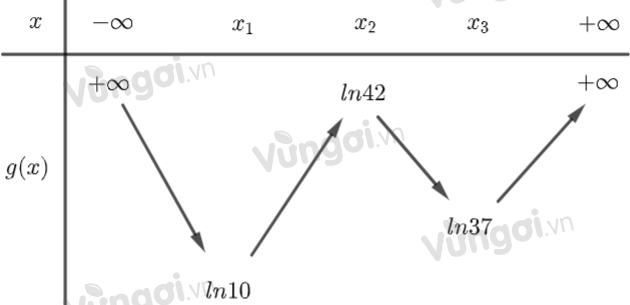
Cho hàm số bậc bốn \(y = f(x)\). Biết rằng hàm số \(g(x) = \ln f(x)\) có bảng biến thiên như sau:

Diện tích hình phẳng giới hạn bởi các đường thẳng $y=f’(x)$ và $y=g’(x)$ thuộc khoảng nào dưới đây?

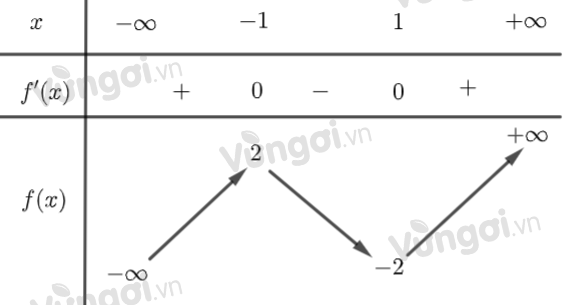
Giả sử \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e\)

Ta có: \(g\left( x \right) = \ln f\left( x \right) \Rightarrow g'\left( x \right) = \dfrac{{f'\left( x \right)}}{{f\left( x \right)}}\)

\(\begin{array}{*{20}{l}}{g\left( {{x_1}} \right) = \ln f\left( {{x_1}} \right) \Rightarrow f\left( {{x_1}} \right) = 10}\\{g\left( {{x_2}} \right) = \ln f\left( {{x_2}} \right) \Rightarrow f\left( {{x_2}} \right) = 42}\\{g\left( {{x_3}} \right) = \ln f\left( {{x_3}} \right) \Rightarrow f\left( {{x_3}} \right) = 37}\end{array}\)

\(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = 0\)

Vì $g’(x) =0$ có 3 nghiệm phân biệt nên $f’(x)=0$ có 3 nghiệm phân biệt và 3 nghiệm đó không là nghiệm của $f(x)=0$.

Vì tập nghiệm của f’(x)=0 trùng với tập nghiệm của g’(x)=0 nên \({x_1},{x_2},{x_3}\) là các điểm cực trị của hàm số y=f(x).

Mà \(f\left( x \right) = {e^{g\left( x \right)}} \Rightarrow \mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) =  + \infty \) =>a>0

Khi đó f(x) có bảng biến thiên

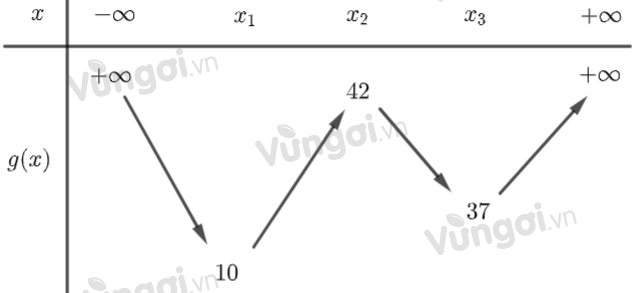
=> \(f(x) - 1 > 0\) với mọi \(x\)

Ta có: \(f'\left( x \right) = g'\left( x \right).f\left( x \right)\) \( \Rightarrow f'\left( x \right) - g'\left( x \right) = g'\left( x \right).\left[ {f\left( x \right) - 1} \right]\)

=> Dấu của \(f{\rm{'}}(x) - g{\rm{'}}(x)\) chỉ phụ thuộc vào dấu của \(g'(x)\)

\(f'\left( x \right) - g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = {x_1}}\\{x = {x_2}}\\{x = {x_3}}\end{array}} \right.\)

Diện tích cần tìm là:

\(\begin{array}{*{20}{l}}{S = \int\limits_{{x_1}}^{{x_3}} {\left| {f'\left( x \right) - g'\left( x \right)} \right|dx} }\\{ = \int\limits_{{x_1}}^{{x_2}} {\left| {f'\left( x \right) - g'\left( x \right)} \right|dx}  + \int\limits_{{x_2}}^{{x_3}} {\left| {f'\left( x \right) - g'\left( x \right)} \right|dx} }\\{ = \int\limits_{{x_1}}^{{x_2}} {\left[ {f'\left( x \right) - g'\left( x \right)} \right]dx}  - \int\limits_{{x_2}}^{{x_3}} {\left[ {f'\left( x \right) - g'\left( x \right)} \right]dx} }\\{ = \left. {f\left( x \right)} \right|_{{x_1}}^{{x_2}} - \left. {g\left( x \right)} \right|_{{x_1}}^{{x_2}} - \left. {f\left( x \right)} \right|_{{x_2}}^{{x_3}} + \left. {g\left( x \right)} \right|_{{x_2}}^{{x_3}}}\\{ = f\left( {{x_2}} \right) - f\left( {{x_1}} \right) - g\left( {{x_2}} \right) + g\left( {{x_1}} \right)}\\{ - f\left( {{x_3}} \right) + f\left( {{x_2}} \right) + g\left( {{x_3}} \right) - g\left( {{x_2}} \right)}\\{ = 2.42 - 10 - 2.\ln 42 + \ln 10 - 37 + \ln 37}\\{ = 37 - 2\ln 42 + \ln 10 + \ln 37}\\{ \approx 35,44 \in \left( {35;36} \right)}\end{array}\)