Trả lời bởi giáo viên
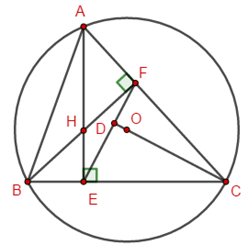
Gọi \(D\) là giao điểm của \(OC\) và \(EF\).
Ta có: \(\left\{ \begin{array}{l}\angle ACO + \angle CAO = {180^0} - \angle AOC\\\angle ACO = \angle CAO\end{array} \right.\) (do tam giác \(OAC\) cân tại \(O\)).
\( \Rightarrow \angle ACO = \angle CAO = {90^0} - \dfrac{1}{2}\angle AOC\,\,\,\left( 1 \right)\)
Mà \(\angle AOC = 2\angle ABC\) (2) (góc nội tiếp và góc ở tâm cùng chắn cung \(AC\)).
\(\angle ABC = \angle DFC\) (3) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp \(ABEF\)).
Từ (1), (2), (3) ta được:
\(\begin{array}{l}\angle ACO = {90^0} - \angle ABC = {90^0} - \angle DFC \Rightarrow \angle ACO + \angle DFC = {90^0}\\ \Rightarrow \angle FDC = {90^0}\end{array}\)
Vậy \(OC \bot EF\).
Hướng dẫn giải:
Chứng minh \(\angle ACO = \angle CAO = {90^0} - \dfrac{1}{2}\angle AOC\,\,\,\left( 1 \right)\)
Mà \(\angle AOC = 2\angle ABC\) (2)
\(\angle ABC = \angle DFC\) (3)
Từ (1), (2) và (3) suy ra được \(\angle FDC = {90^0}\)
Câu hỏi khác
- Đề thi chính thức vào 10 môn Toán Sở GD&ĐT Thành phố Hà Nội (Năm học 2021 - 2022) - có lời giải chi tiết
- Đề thi chính thức vào 10 môn Toán Sở GD&ĐT Tỉnh Hải Dương (2021 - 2022) có lời giải chi tiết
- Đề thi chính thức vào 10 môn Toán Sở GD&ĐT TP Đà Nẵng (2021 - 2022) có lời giải chi tiết
- Đề thi chính thức vào 10 môn Toán Sở GD&ĐT Tỉnh Bình Dương (2021 - 2022) có lời giải chi tiết
- Đề thi chính thức vào 10 môn Toán Sở GD&ĐT Tỉnh Thái Bình (2021 - 2022) có lời giải chi tiết
