Câu hỏi:
2 năm trước
Cho tứ giác \(ABCD\). Gọi \(E\), \(F\) lần lượt là trung điểm của \(AB\) và \(CD.\)\(M,N,P,Q\) lần lượt là trung điểm của \(AF,CE,BF,DE\). Khi đó \(MNPQ\) là hình gì? Chọn đáp án đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: a
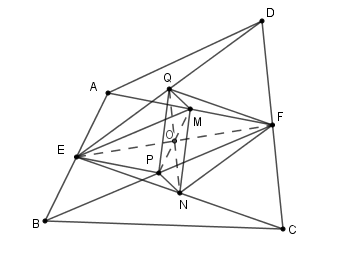
Nối \(EF;EP,FQ,EM,PM,QN\). Gọi \(O\) là giao của \(QN\) và \(EF\).
Xét tam giác \(CED\) có \(FN\) là đường trung bình nên \(\left\{ \begin{array}{l}FN = \dfrac{1}{2}DE = EQ\\FN//ED\end{array} \right. \Rightarrow NFQE\) là hình bình hành nên hai đường chéo \(QN\) và \(EF\) giao nhau tại trung điểm của mỗi đường. Suy ra \(O\) là trung điểm của \(QN\) (1) và \(EF\).
Xét tam giác \(ABF\) có \(EM\) là đường trung bình nên \(\left\{ \begin{array}{l}EM = \dfrac{1}{2}BF = PF\\EM//PF\end{array} \right. \Rightarrow EMFB\) là hình bình hành nên hai đường chéo \(PM\) và \(EF\) giao nhau tại trung điểm của mỗi đường. Mà \(O\) là trung điểm của \(EF\) nên \(O\) cũng là trung điểm của \(PM\) (2)
Từ (1) và (2) suy ra: tứ giác \(QMNP\) có hai đường chéo \(QN,PM\) giao nhau tại trung điểm \(O\) mỗi đường nên \(QMNP\) là hình bình hành (dhnb).
Hướng dẫn giải:
Bước 1: Sử dụng tính chất đường trung bình của tam giác để chứng minh các cạnh song song và bằng nhau.
Bước 2: Sử dụng dấu hiệu nhận biết “tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường”.
