Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\) có các cạnh \(AB,AC,AD\) đôi một vuông góc với nhau, \(AB = 6a,AC = 7a,AD = 4a\). Gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(BC,CD,DB\). Thể tích \(V\) của tứ diện \(AMNP\) là:
Trả lời bởi giáo viên
Đáp án đúng: d
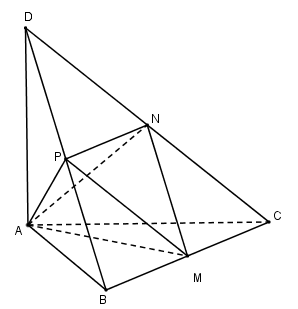
Ta có:
\(ABCD\) là tứ diện vuông tại \(A\) nên \({V_{ABCD}} = \dfrac{1}{6}AB.AC.AD = \dfrac{1}{6}.6a.7a.4a = 28{a^3}\).
Áp dụng công thức tính tỉ lệ thể tích các khối tứ diện ta có:
\(\dfrac{{{V_{DAPN}}}}{{{V_{DABC}}}} = \dfrac{{DA}}{{DA}}.\dfrac{{DP}}{{DB}}.\dfrac{{DN}}{{DC}} = \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{DAPN}} = \dfrac{1}{4}{V_{DABC}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
\(\dfrac{{{V_{BAPM}}}}{{{V_{BADC}}}} = \dfrac{{BA}}{{BA}}.\dfrac{{BP}}{{BD}}.\dfrac{{BM}}{{BC}} = \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{BAPM}} = \dfrac{1}{4}{V_{BADC}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
\(\dfrac{{{V_{CAMN}}}}{{{V_{CABD}}}} = \dfrac{{CA}}{{CA}}.\dfrac{{CM}}{{CB}}.\dfrac{{CN}}{{CD}} = \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{CAMN}} = \dfrac{1}{4}{V_{CABD}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
Do đó \({V_{AMNP}} = {V_{ABCD}} - {V_{DAPN}} - {V_{BAPM}} - {V_{CAMN}} = 28{a^3} - 7{a^3} - 7{a^3} - 7{a^3} = 7{a^3}\)
Hướng dẫn giải:
Tính thể tích các khối chóp ${{V_{DAPN}}}$, ${{V_{BAPM}}}$, ${V_{CAMN}}$ và $ V_{ABCD}$ rồi tính ${V_{AMNP}} = {V_{ABCD}} - {V_{DAPN}} $ $- {V_{BAPM}} - {V_{CAMN}}$
Giải thích thêm:
- Một số em sẽ tính nhầm tỉ lệ thể tích khối tứ diện \(AMNP\) và \(ABCD\) là \(\dfrac{1}{3}\) nên chọn nhầm đáp án C là sai.
- Cách giải ở trên hướng dẫn các em tính thể tích tứ diện bằng phương pháp cộng trừ thể tích (phân chia khối đa diện) và cách áp dụng công thức tỉ lệ thể tích.
Ngoài ra, bài toán còn một cách giải khác, các em có thể tham khảo các bước giải như sau:
+ Tính thể tích của tứ diện \(ABCD\)
+ So sánh diện tích các tam giác \(MNP\) và \(BCD\), cụ thể \({S_{MNP}} = \dfrac{1}{4}{S_{BCD}}\)
+ So sánh thể tích \({V_{A.MNP}}\) và \({V_{A.BCD}}\), cụ thể:
Hai tứ diện có chung chiều cao kẻ từ \(A\) và diện tích đáy \({S_{MNP}} = \dfrac{1}{4}{S_{BCD}}\)
Do đó \({V_{A.MNP}} = \dfrac{1}{4}{V_{A.BCD}}\)
Câu hỏi khác
- Đề thi kiểm tra giữa học kì 1 - Đề số 5 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 3 Toán 12 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 đề số 2 Toán 12 có lời giải chi tiết
