Câu hỏi:
2 năm trước
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Các tiếp tuyến tại \(B,C\) của \(\left( O \right)\) cắt nhau tại \(M\). Biết \(\widehat {BAC} = 2\widehat {BMC}\). Tính \(\widehat {BAC}\) .
Trả lời bởi giáo viên
Đáp án đúng: c
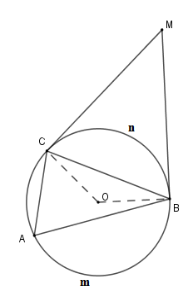
Xét \(\left( O \right)\) có
\(\widehat {BMC} \) \(= \dfrac{1}{2}\) (sđ \(\overparen{BmC} - \) sđ \(\overparen{BnC}\) ) (góc có đỉnh bên ngoài đường tròn)
Và \(\widehat {BAC} = \dfrac{1}{2}\) sđ \(\overparen{BnC}\)
Mà \(\widehat {BAC} = 2\widehat {BMC}\) nên
(sđ \(\overparen{BmC} - \) sđ \(\overparen{BnC}\) )\( = \dfrac{1}{2}\) sđ \( \overparen{BnC}\)
\( \Rightarrow \) sđ \(\overparen{BmC} = \) \(\dfrac{3}{2}\). sđ \(\overparen{BnC}\)
mà sđ \(\overparen{BmC} + \) sđ \(\overparen{BnC}\)$ = 360^\circ $
Nên sđ \(\overparen{BnC}=\) \(\dfrac{{2.360^\circ }}{5} = 144^\circ \) , do đó \(\widehat {BAC} = \dfrac{{120^\circ }}{2} = 72^\circ \) .
Hướng dẫn giải:
Sử dụng góc nội tiếp và góc có đỉnh bên ngoài đường tròn
