Trả lời bởi giáo viên
Đáp án đúng: d
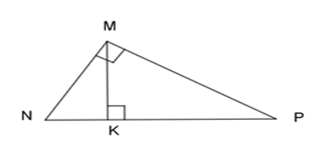
+) Xét 2 tam giác vuông $\Delta KNM$ và $\Delta MNP$ có: \(\widehat N\) chung
nên $\Delta KNM$\( \backsim \) $\Delta MNP$ (g.g) (1)
Xét 2 tam giác vuông $\Delta KMP$ và $\Delta MNP$ có: \(\widehat P\) chung
nên $\Delta KMP$\( \backsim \) $\Delta MNP$ (g.g) (2)
Từ (1) và (2) suy ra: $\Delta KNM$ \( \backsim \) $\Delta KMP$ (theo t/c bắc cầu).
Vậy $\Delta KNM$\( \backsim \) $\Delta MNP$\( \backsim \)$\Delta KMP$ nên A đúng.
+) Theo chứng minh trên: $\Delta KNM$ \( \backsim \) $\Delta KMP.$
\( \Rightarrow \dfrac{{MK}}{{PK}} = \dfrac{{NK}}{{MK}}\)
\( \Leftrightarrow M{K^2} = NK.PK\) nên B đúng.
Vậy cả A, B đều đúng.
Hướng dẫn giải:
- Áp dụng phương pháp chứng minh tam giác đồng dạng và biến đổi tỉ lệ thức để thực hiện yêu cầu của bài toán.