Cho tam giác \(ABC\) vuông tại \(A,\) điểm \(M\) thuộc cạnh huyền \(BC.\) Gọi \(D,E\) lần lượt là chân đường vuông góc kẻ từ \(M\) đến \(AB,AC.\)

Tính độ dài nhỏ nhất của \(DE\) khi \(M\) di chuyển trên BC biết \(AB = 15cm;AC = 20cm.\)

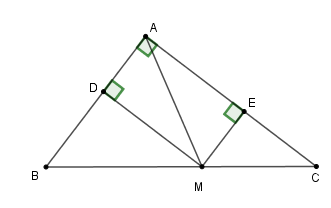
Theo \(DE\) nhỏ nhất khi \(M\) là hình chiếu của \(A\) trên \(BC.\) Khi đó \(DE = AM.\)

Xét tam giác \(ABC\), theo định lý Pyatgo ta có \(B{C^2} = A{B^2} + A{C^2} = 625 \Rightarrow BC = 25\).

Gọi \(BM = x\) thì \(MC = 25 - x\).

Xét tam giác \(AMB\) vuông tại \(M\), theo định lý Pytago ta có \(A{M^2} = A{B^2} - B{M^2} = {15^2} - {x^2} = 225 - {x^2}\) (1)

Xét tam giác \(AMC\) vuông tại \(M,\) theo định lý Pytago ta có \(A{M^2} = A{C^2} - M{C^2} = {20^2} - {\left( {25 - x} \right)^2}\)  (2)

Từ (1) và (2) suy ra: \(225 - {x^2} = {20^2} - {\left( {25 - x} \right)^2}\)\( \Leftrightarrow 225 - {x^2} = 400 - \left( {625 - 50x + {x^2}} \right)\)\( \Leftrightarrow 50x = 450 \Leftrightarrow x = 9\).

Suy ra: \(A{M^2} = 225 - {x^2} = 225 - 81 = 144 \Rightarrow AM = 12\) suy ra \(DE = AM = 12cm\).

Vậy giá trị nhỏ nhất của \(DE\) là \(12cm.\)