Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông tại \(A,\) điểm \(M\) thuộc cạnh huyền \(BC.\) Gọi \(D,E\) lần lượt là chân đường vuông góc kẻ từ \(M\) đến \(AB,AC.\)
Điểm \(M\) ở vị trí nào trên \(BC\) thì \(DE\) có độ dài nhỏ nhất?
Trả lời bởi giáo viên
Đáp án đúng: a
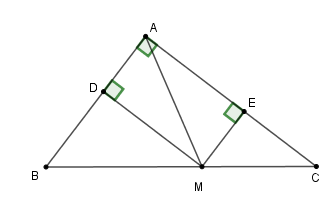
Vì \(ADME\) là hình chữ nhật (theo câu trước) nên \(AM = DE\) (tính chất)
Để \(DE\) nhỏ nhất thì \(AM\) nhỏ nhất mà \(AM\) nhỏ nhất khi \(M\) là hình chiếu của \(A\) trên \(BC.\)
Từ đó \(DE\) nhỏ nhất khi \(M\) là hình chiếu của \(A\) trên \(BC.\)
Hướng dẫn giải:
Sử dụng tính chất hình chữ nhật và mối quan hệ giữa đường vuông góc và đường xiên.

