Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) với ba trung tuyến \(AI,BD,CE\) đồng quy tại \(G.\) \(M\) và \(N\) lần lượt là trung điểm của \(GC\) và \(GB.\)
Để \(MNED\) là hình chữ nhật thì tam giác \(ABC\) cần có điều kiện:
Trả lời bởi giáo viên
Đáp án đúng: c
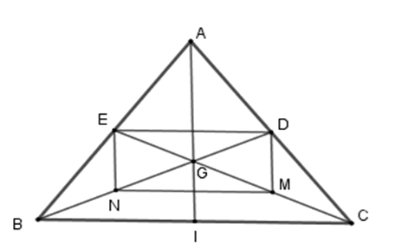
+ Xét tam giác \(ABG\) có \(EN\) là đường trung bình nên \(EN{\rm{//}}AG\) hay \(EN{\rm{//}}AI\).
+ Để hình bình hành \(MNED\) là hình chữ nhật thì \(\widehat {ENM} = 90^\circ \Rightarrow EN \bot MN\) . Mà \(MN{\rm{//}}BC\) (câu a) nên \(EN \bot BC\).
+ Lại có \(EN{\rm{//}}AI\) suy ra \(AI \bot BC\) .
Xét tam giác \(ABC\) có \(AI\) vừa là đường cao vừa là trung tuyến nên \(\Delta ABC\) cân tại \(A\) .
Hướng dẫn giải:
Bước 1: Chứng minh \(EN{\rm{//}}AI\) bằng tính chất đường trung bình.
Bước 2: Sử dụng dấu hiệu nhận biết “hình bình hành có một góc vuông là hình chữ nhật” để suy ra \(EN \bot NM\) .
Bước 3: Sử dụng quan hệ từ vuông góc đến song song để suy ra \(AI\) vừa là đường cao vừa là trung tuyến nên \(\Delta ABC\) cân tại \(A\) .
