Câu hỏi:
2 năm trước
Cho tam giác $ABC$ với ba đường cao $AA';\,BB';\,CC'$ . Gọi $H$ là trực tâm của tam giác đó. Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: a
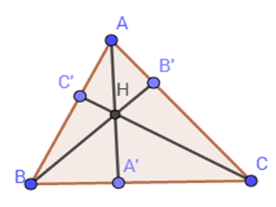
Ta có:
\(\begin{array}{l}{S_{HBC}} + {S_{HAC}} + {S_{HAB}} = {S_{ABC}}\\ \Rightarrow \dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} + \dfrac{{{S_{HAC}}}}{{{S_{ABC}}}} + \dfrac{{{S_{HAB}}}}{{{S_{ABC}}}} = 1\\ \Leftrightarrow \dfrac{{HA'.BC}}{{AA'.BC}} + \dfrac{{HB'.AC}}{{BB'.AC}} + \dfrac{{HC'.BA}}{{CC'.BA}} = 1\\ \Leftrightarrow \dfrac{{HA'}}{{AA'}} + \dfrac{{HB'}}{{BB'}} + \dfrac{{HC'}}{{CC'}} = 1\,\,\,\,\left( {đpcm} \right).\end{array}\)
Hướng dẫn giải:
Lập công thức tính diện tích tam giác ABC theo tổng diện tích của ba tam giác HBC; HAC; HAB. Từ đó biến đổi để dẫn đến hệ thức cần tìm.

