Cho tam giác \(ABC\), phân giác \(AD\). Gọi \(E,F\) lần lượt là hình chiếu của \(B\) và \(C\) lên \(AD\).

Chọn khẳng định không đúng.

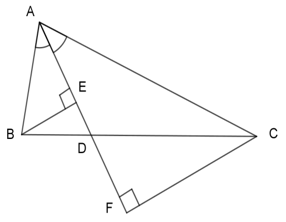
Xét 2 tam giác vuông ABE và ACF ta có:

\(\widehat {BAE} = \widehat {CAF}\) (vì AD là tia phân giác của góc A)

\( \Rightarrow \Delta ABE\backsim\Delta ACF\;(g - g)\)

\( \Rightarrow \dfrac{{AE}}{{AF}} = \dfrac{{BE}}{{CF}}\;(1)\)\( \Rightarrow AE.CF = AF.BE\) hay A đúng.

Xét 2 tam giác vuông BDE và CDF ta có:

\(\widehat {EDB} = \widehat {FDC}\) (2 góc đối đỉnh)

\( \Rightarrow \Delta BDE\backsim\Delta CDF\) (g – g)

\( \Rightarrow \dfrac{{BE}}{{CF}} = \dfrac{{DE}}{{DF}}\;(2)\) hay D đúng.

Từ (1) và (2) ta có:

\(\dfrac{{AE}}{{AF}} = \dfrac{{DE}}{{DF}} \Leftrightarrow AE.DF = AF.DE\) hay C đúng.