Câu hỏi:
2 năm trước
Cho tam giác \(ABC\). Một đường tròn tâm \(O\) nội tiếp tam giác \(ABC\) và tiếp xúc với \(BC\) tại \(D\). Đường tròn tâm \(I\) là đường tròn bàng tiếp trong góc \(A\) của tam giác \(ABC\) và tiếp xúc với \(BC\) tại \(F\). Vẽ đường kính \(DE\) của đường tròn \(\left( O \right)\). Chọn đáp án đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: d
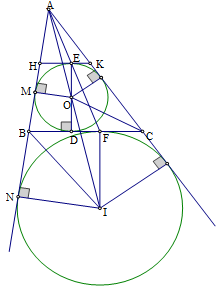
Theo đề ra có \(A,O,I\) thẳng hàng (vì \(O,I\) cùng nằm trên tia phân góc \(A\)).
+ Gọi \(M,N\) là tiếp điểm của \(\left( O \right)\); \(\left( I \right)\) với \(AB\), ta có \(OM//IN\) nên \(\dfrac{{AO}}{{AI}} = \dfrac{{OM}}{{IN}}\) (hệ quả của định lý Thales).
Mà \(OM = OE,IN = IF\) nên có \(\dfrac{{AO}}{{AI}} = \dfrac{{OE}}{{IF}}\).
Mặt khác \(ED \bot BC,IF \bot BC\)\( \Rightarrow OD//IF \Rightarrow \widehat {AOE} = \widehat {AIF}\).
+ Xét \(\Delta OAE\) và \(\Delta IAF\) có \(\dfrac{{AO}}{{AI}} = \dfrac{{OE}}{{IF}};\widehat {AOE} = \widehat {AIF}\),
do đó \(\Delta OAE \backsim \Delta IAF \Rightarrow \widehat {OAE} = \widehat {IAF}\).
Vậy \(A,E,F\) thẳng hàng.
Hướng dẫn giải:
Sử dụng hệ quả của định lý Ta-lét, tính chất hai đường thẳng song song và hai tam giác đồng dạng.
Chú ý rằng tâm đường tròn bàng tiếp tam giác là giao hai đường phân giác góc ngoài và \(1\) đường phân giác góc trong của tam giác.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
