Cho tam giác \(ABC.\) Gọi \(D\) là điểm đối xứng với \(B\) qua \(A,E\) là điểm đối xứng với \(C\) qua \(A.\) Lấy các điểm \(I;K\) theo thứ tự thuộc các đoạn thẳng \(DE,BC\) sao cho \(DI = BK.\) Chọn câu đúng.

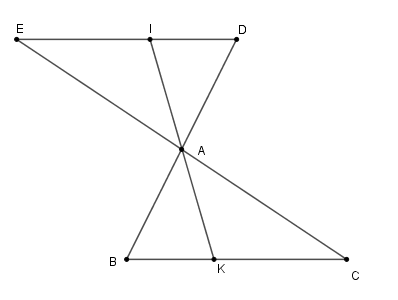
Xét \(\Delta ADE\) và \(\Delta ABC\) có:

+  \(AD = AD\) (vì \(D\) đối xứng với \(B\) qua \(A\) )

+ \(\widehat {EAD} = \widehat {BAC}\) (đối đỉnh)

+ \(AE = AC\) (vì \(E\) đối xứng với \(C\) qua \(A\))

Nên \(\Delta ADE = \Delta ABC\left( {c - g - c} \right)\), suy ra \(\widehat {EDA} = \widehat {ABC}\) mà hai góc này ở vị trí so le trong nên \(ED//BC\).

Xét \(\Delta ADI\) và \(\Delta ABK\) có:

+ \(AD = AB\) (vì \(D\) đối xứng với \(B\) qua \(A\) )

+ \(\widehat {EDA} = \widehat {ABC}\) (cmt)

+ \(DI = BK\left( {gt} \right)\)

Nên \(\Delta ADI = \Delta ABK\,\left( {c - g - c} \right)\) \( \Rightarrow \widehat {IAD} = \widehat {KAB}\) mà \(B,A,D\) thẳng hàng nên \(K,A,I\) thẳng hàng.

Lại có \(IA = AK\) (do \(\Delta ADI = \Delta ABK\)) nên điểm \(K\) đối xứng với \(I\) qua \(A.\)