Câu hỏi:
2 năm trước
Cho tam giác \(ABC\), điểm \(M\) thuộc cạnh \(BC\) sao cho \(\dfrac{{MB}}{{MC}} = \dfrac{1}{2}.\) Đường thẳng đi qua M và song song với \(AC\) cắt \(AB\) ở \(D\). Đường thẳng đi qua \(M\) và song song với \(AB\) cắt \(AC\) ở\(E\). Tỉ số chu vi hai tam giác \(\Delta DBM\) và \(\Delta EMC\) là:
Trả lời bởi giáo viên
Đáp án đúng: a
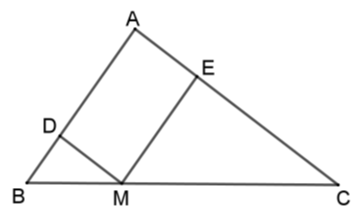
Ta có: \(MD\) // \(AC\) nên \(\Delta DBM\backsim\Delta ABC\).
Suy ra \(\dfrac{{DB}}{{AB}} = \dfrac{{BM}}{{BC}} = \dfrac{{DM}}{{AC}}\) \( = \dfrac{{DB + BM + DM}}{{AB + BC + AC}}\)
Do đó \(\dfrac{1}{3} = \dfrac{{{P_{\Delta BDM}}}}{{{P_{\Delta ABC}}}}\,\,\,\left( 1 \right)\)
Ta có: \(ME\) // \(AB\) nên \(\Delta EMC\backsim\Delta ABC.\) Suy ra
\(\dfrac{{EM}}{{AB}} = \dfrac{{MC}}{{BC}} = \dfrac{{EC}}{{AC}}\) \( = \dfrac{{EM + MC + EC}}{{AB + BC + AC}}\)
Do đó \(\dfrac{2}{3} = \dfrac{{{P_{\Delta {\rm E}{\rm M}C}}}}{{{P_{\Delta ABC}}}}\,\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra: \(\dfrac{{{P_{\Delta BDM}}}}{{{P_{\Delta ABC}}}}:\dfrac{{{P_{\Delta EMC}}}}{{{P_{\Delta ABC}}}} = \dfrac{1}{3}:\dfrac{2}{3}\) \( \Leftrightarrow \dfrac{{{P_{\Delta BDM}}}}{{{P_{\Delta EMC}}}} = \dfrac{1}{2}\).
Hướng dẫn giải:
+ Sử dụng định lý về tam giác đồng dạng để suy ra các tam giác đồng dạng.
+ Từ các cạnh tương ứng tỉ lệ và tính chất tỉ lệ thức suy ra tỉ số chu vi hai tam giác.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
