Cho tam giác \(ABC\) có ba góc nhọn. Kẻ các đường cao \(BE,CF\). Trên đoạn thẳng \(BE\), lấy điểm \(M\) sao cho \(\Delta AMC\) vuông tại \(M\). Trên đoạn thẳng \(CF\), lấy điểm \(N\) sao cho \(\Delta ANB\) vuông tại \(N\).

Chọn câu đúng.

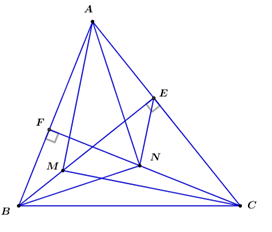
Xét tứ giác \(ABNE\) có: \(\widehat {ANB} = \widehat {AEB} = {90^o}\). Suy ra hai điểm \(N,E\) cùng nhìn cạnh \(AB\) với hai góc bằng nhau. Suy ra \(ABNE\) nội tiếp đường tròn.

Xét đường tròn ngoại tiếp tứ giác \(ABNE\) có \(\widehat {ANE},\widehat {ABE}\) là hai góc nội tiếp cùng chắn cung \(AE\). Suy ra  \(\widehat {ANE} = \widehat {ABE}\)

Mà có \(\widehat {ABE} = \widehat {ACF}\) (do cùng phụ với \(\widehat {BAC}\) )

\( \Rightarrow \widehat {ANE} = \widehat {ACF}\)

Xét \(\Delta ANE\) và \(\Delta ACN\) có

+) \(\widehat {NAC}\) chung

+) \(\widehat {ANE} = \widehat {ACF}\) ( chứng minh trên )

\( \Rightarrow \Delta ANE \backsim \Delta ACN\left( {g - g} \right) \Rightarrow \dfrac{{AN}}{{AC}} = \dfrac{{AE}}{{AN}} \Rightarrow A{N^2} = AE.AC\).                            (1)

Chứng minh tương tự có: \(A{M^2} = FA.AB\).                                                      (2)

Xét $\Delta CFA$ và \(\Delta BEA\) có:

+) \(\widehat {BAC}\) chung

+) \(\widehat {AEB} = \widehat {CFA} = {90^0}\)

\( \Rightarrow \Delta CFA \backsim \Delta BEA\left( {g - g} \right) \Rightarrow \dfrac{{FA}}{{EA}} = \dfrac{{AC}}{{AB}} \Rightarrow FA.AB = EA.AC\)                               (3)

Từ (1), (2), (3) \( \Rightarrow A{N^2} = A{M^2} \Rightarrow AN = AM\)

Vậy cả A, C đều đúng.