Cho tam giác \(ABC\) có \({90^0} < \widehat B < {135^0};\,\widehat C < {45^0}.\) Vẽ đường cao \(AH.\) Chọn câu đúng.

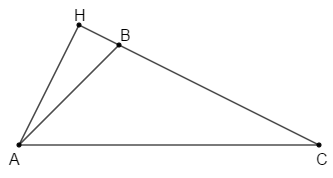
Ta có \(\widehat {ABC} + \widehat {ABH} = {180^o}\) (hai góc kề bù), mà \(\widehat {ABC} < {135^o}\,(gt)\) suy ra \(\widehat {ABH} > {180^o} - {135^o} = {45^o}\)        (1)

\(\Delta AHB\) có \(\widehat {AHB} = {90^o}\) nên \(\widehat {ABH} + \widehat {BAH} = {90^o}\), mà \(\widehat {ABH} > {45^o}\,(cmt)\) suy ra \(\widehat {BAH} < {90^o} - {45^o} = {45^o}\)    (2)

Từ (1) và (2) ta có \(\widehat {ABH} > \widehat {BAH}\) suy ra \(AH > BH\)        (3)

\(\Delta AHC\) có \(\widehat {AHC} = {90^o}\) nên \(\widehat {CAH} + \widehat C = {90^o}\), mà \(\widehat C < {45^o}\,(gt)\) nên \(\widehat {CAH} > {90^o} - {45^o} = {45^o}\). Từ đó suy ra \(\widehat C < \widehat {CAH}\) suy ra \(AH < CH\)        (4)

Từ (3) và (4) suy ra \(BH < AH < CH.\)