Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) cân tại \(A\). Đường thẳng qua \(C\) và vuông góc \(AB\) tại \(CE\). Tính \(AB\), biết \(BC = 18\) cm và \(BE = 6,75\)cm.
Trả lời bởi giáo viên
Đáp án đúng: c
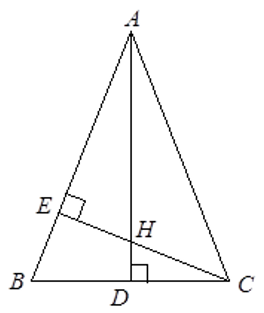
Kẻ đường cao \(AD\). Xét \(\Delta CBE\) và \(\Delta ABD\) có: \(\widehat {BEC} = \widehat {ADB} = 90^\circ \) và \(\widehat B\) chung nên
\(\Delta CBE\backsim\Delta ABD\) (g.g) \( \Rightarrow \dfrac{{BC}}{{AB}} = \dfrac{{BE}}{{BD}}\) hay \(\dfrac{{18}}{{AB}} = \dfrac{{6,75}}{9}\)
\( \Rightarrow AB = 24{\rm{cm}}\).
Hướng dẫn giải:
- Kẻ đường cao \(AD\) sau đó chứng minh hai tam giác đồng dạng để suy ra tỉ lệ cạnh thích hợp, từ đó tính \(AB\).
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
