Cho tam giác $ABC{\rm{ }}\left( {AB{\rm{ }} < {\rm{ }}AC} \right)$ có các góc đều nhọn, các đường cao $AD,{\rm{ }}BE,{\rm{ }}CF$  cắt nhau tại $H.$ Đường thẳng $EF$ cắt đường thẳng $BC$ và  $AD$ lần lượt tại $K$ và $I.$  Qua $F$ kẻ đường thẳng song song với $AC$ cắt $AK,{\rm{ }}AD$ lần lượt tại $M$ và $N.$ Gọi $O$ là trung điểm của $BC.$ Chọn câu đúng.

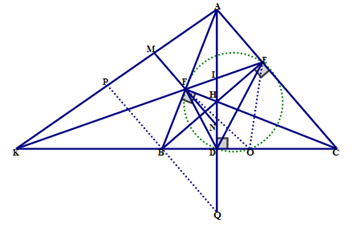
*) Dễ chứng minh tứ giác BDHF nội tiếp đường tròn đường kính HB (1) và tứ giác ABDE nội tiếp đường tròn đường kính AB (2)

(1) $ \Rightarrow \widehat {HDF} = \widehat {HBF}$(nội tiếp cùng chắn cung HF) (1’),

(2) $ \Rightarrow \widehat {HBF} = \widehat {HDE}$(2’) (nội tiếp cùng chắn cung AF)

(1’) và (2’) suy ra: $\widehat {HDF} = \widehat {HDE}$

Vậy DA là phân giác của $\widehat {FDE}$  nên A đúng.

*) Qua B kẻ đường thẳng song song với AC cắt AK, AD tại P, Q  \( \Rightarrow \) PQ // MN // AC

Ta có: FC là phân giác của $\widehat {DFE}$(tương tự chứng minh câu a)

mà FB \( \bot \) FC nên PB là phân giác trong và FC là phân giác ngoài \(\Delta \)KFD

\( \Rightarrow \,\,\dfrac{{{\rm{BK}}}}{{{\rm{BD}}}}\,\,{\rm{ = }}\,\,\dfrac{{FK}}{{FD}} = \dfrac{{{\rm{CK}}}}{{{\rm{CD}}}}\,\, \Rightarrow \,\,\dfrac{{{\rm{KB}}}}{{{\rm{KC}}}}\,\,{\rm{ = }}\,\,\dfrac{{{\rm{DB}}}}{{{\rm{DC}}}}\)       (3)

Theo hệ quả của định lí Ta-let, ta lại có:

       \(\dfrac{{{\rm{BP}}}}{{{\rm{CA}}}}\,\,{\rm{ = }}\,\,\dfrac{{{\rm{KB}}}}{{{\rm{KC}}}}\) (4)     (vì BP // AC)   

        và: \(\,\,\dfrac{{{\rm{BQ}}}}{{{\rm{CA}}}}\,\,{\rm{ = }}\,\,\dfrac{{{\rm{DB}}}}{{{\rm{DC}}}}\) (5)     (BQ // AC)

Từ (3), (4), (5) suy ra: \(\dfrac{{{\rm{BP}}}}{{{\rm{CA}}}}\,\,{\rm{ = }}\,\,\dfrac{{{\rm{BQ}}}}{{{\rm{AC}}}}\,\,\)\( \Rightarrow \) BP = BQ

Khi đó, áp dụng hệ quả của định lí Ta-let trong hai tam giác ABP và ABQ  với MF // PQ, NF // BQ, có:

$\dfrac{{{\rm{MF}}}}{{{\rm{BP}}}}\,{\rm{ = }}\,\dfrac{{{\rm{AF}}}}{{{\rm{AB}}}}\,{\rm{ = }}\,\dfrac{{{\rm{FN}}}}{{{\rm{BQ}}}}\, \Leftrightarrow \,\dfrac{{MF}}{{BQ}}{\rm{ = }}\dfrac{{{\rm{FN}}}}{{{\rm{BQ}}}} \Leftrightarrow {\rm{MF}}\,{\rm{ = }}\,{\rm{NF}}\, \Rightarrow $ F là trung điểm của MN nên B đúng

+) Vì DA là phân giác của $\widehat {FDE}$  \( \Rightarrow \,\,\widehat {{\rm{DFE}}}\,\,{\rm{ = }}\,\,{\rm{2}}\widehat {{\rm{CFE}}}\) (6)

Dễ chứng minh tứ giác BCEF nội tiếp đường tròn

(O) đường kính BC,  

nên \(\widehat {{\rm{EOC}}}\,\,{\rm{ = }}\,\,{\rm{2}}\widehat {{\rm{CFE}}}\)    (7)

Từ (6) và (7) suy ra: \(\widehat {{\rm{DFE}}}\,\,{\rm{ = }}\,\,\widehat {{\rm{EOC}}}\,\, \Rightarrow \) Tứ giác DFEO nội tiếp

$ \Rightarrow \widehat {ODE} = \dfrac{1}{2}$sđ cung \(OE\)=$\dfrac{1}{2}$sđ cung\(\,OF\)= \(\widehat {{\rm{OEK}}}\) (vì OE = OF = $\dfrac{{\rm{1}}}{{\rm{2}}}$BC)

Từ đó suy ra: \(\Delta ODE \backsim \Delta OEK\) (g.g) \(\dfrac{{OE}}{{OK}} = \dfrac{{OD}}{{OE}} \Rightarrow \,\,{\rm{OD}}{\rm{.OK}}\,\,{\rm{ = }}\,\,{\rm{O}}{{\rm{E}}^{\rm{2}}}\)

Khi đó:

\(\begin{array}{l}{\rm{BD}}{\rm{.DC}}\,\,{\rm{ = }}\,\,\left( {{\rm{OB}}\,\, - \,\,{\rm{OD}}} \right)\left( {{\mathop{\rm OC}\nolimits} \,\, + \,\,OD} \right)\,\, = \,\,{\rm{O}}{{\rm{B}}^2}\, - \,\,{{\mathop{\rm OD}\nolimits} ^2}\, = \,\,{\rm{OD}}{\rm{.OK}}\,\, - \,\,{\rm{O}}{{\rm{D}}^{\rm{2}}}\,\,\\ = \,\,{\rm{OD}}\left( {{\rm{OK}}\,\, - \,\,{\rm{OD}}} \right)\,\, = \,\,{\rm{OD}}{\rm{.DK}}\end{array}\)

Nên C đúng.

Vậy cả A, B, C đều đúng.