Câu hỏi:
2 năm trước
Cho \(\left( {O;R} \right)\) có hai đường kính \(AB,CD\) vuông góc với nhau. Gọi \(M\) là điểm chính giữa cung \(BC\) . Dây \(AM\) cắt \(OC\) tại \(E\) , dây \(CM\) cắt đường thẳng \(AB\) tại \(N\) .
Hai đoạn thẳng nào sau đây bằng nhau?
Trả lời bởi giáo viên
Đáp án đúng: a
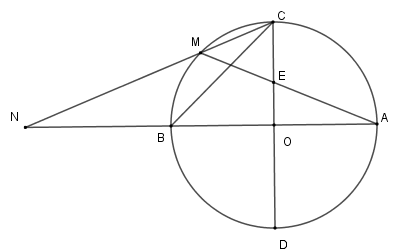
Xét \(\left( O \right)\) có \(\widehat {CNA}\) là góc có đỉnh bên ngoài đường tròn nên
\(\widehat {CNB} = \dfrac{1}{2}\) $ (sđ \overparen{AC}-sđ \overparen{MB})$
Mà sđ $\overparen{MB}$\( = \dfrac{1}{2}\) sđ $\overparen{AC}$ nên \(\widehat {CNA} = \dfrac{1}{2}\)sđ $\overparen{MB}$
Lại có \(\widehat {MCB} = \dfrac{1}{2}\) sđ $\overparen{MB}$ (góc nội tiếp) nên \(\widehat {MCB} = \widehat {BNC} \Rightarrow \Delta BNC\) cân tại \(B \Rightarrow BN = BC\) .
Hướng dẫn giải:
Sử dụng góc nội tiếp và góc có đỉnh bên ngoài đường tròn
