Câu hỏi:
2 năm trước
Cho nửa đường tròn tâm $O$ đường kính $AB.$ Vẽ các tiếp tuyến $Ax$ và $By$ ($Ax$ và $By$ và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là $AB$ ). Gọi $M$ là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại $M$ cắt $Ax$ và $By$ theo thứ tự tại $C$ và $D.$
Tìm vị trí điểm $C$ và $D$ để hình thang $ABDC$ có chu vi bằng $14,$ biết $AB = 4{\rm{ }}cm.$
Trả lời bởi giáo viên
Đáp án đúng: a
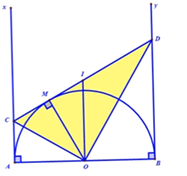
Gọi \(I\) là trung điểm của $CD$
Suy ra $I$ là tâm của đường tròn đường kính $CD$
Theo tính chất hai tiếp tuyến cắt nhau: $AC = CM\;$ và $BD = DM$
Xét tứ giác $ABDC$ có: $AC//BD \Rightarrow ABDC$ là hình thang
\( \Rightarrow \,IO\) là đường trung bình của hình thang $ABDC$
\( \Rightarrow IO//AC//BD\) mà $AC\; \bot AB{\rm{ }} \Rightarrow IO\; \bot AB{\rm{ }}\left( 1 \right)$
$IO = \dfrac{{AC + BD}}{2} = \dfrac{{CM + DM}}{2} = \dfrac{{CD}}{2}(2)$
Suy ra tam giác \(COD\) vuông tại \(O.\)
${C_{ABDC}} = 14 \Leftrightarrow AB + 2CD = 14 \Rightarrow CD = \dfrac{{14 - AB}}{2} = \dfrac{{14 - 4}}{2} = 5cm$
Lại có: $CD = CM + DM = AC + BD \Rightarrow AC = CD-BD = 5-BD$
Mà tam giác \(COD\) vuông tại \(O.\)
Áp dụng hệ thức lượng vào tam giác vuông $COD$ ta có:
$O{M^2} = {\rm{ }}CM.DM \Leftrightarrow {2^2} = AC.BD \Leftrightarrow AC.BD = 4 \Leftrightarrow \left( {5 - BD} \right).BD = 4$
\( \Leftrightarrow 5BD--B{D^2} = 4 \Leftrightarrow B{D^2}--5BD + 4 = 0\)
\( \Leftrightarrow B{D^2}-BD-4BD + 4 = 0 \Leftrightarrow BD\left( {BD-1} \right)-4\left( {BD-1} \right) = 0\)
\( \Leftrightarrow \left( {BD - 1} \right)\left( {BD - 4} \right) = 4\)
$ \Leftrightarrow \left[ \begin{array}{l}BD - 1 = 0\\BD - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}BD = 1 \Rightarrow AC = 4\\BD = 4 \Rightarrow AC = 1\end{array} \right.$
Vậy với $AC = 4cm;BD = 1cm$ hoặc $AC = 1{\rm{ }}cm;BD = 4cm$ thì chu vi của hình thang $ABDC$ bằng $14.$
Hướng dẫn giải:
+ Tính \(CD\) dựa vào chu vi \(ABCD.\)
+ Tính \(BD\) dựa vào hệ thức lượng, từ đó tính \(AC.\)
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
