Câu hỏi:
2 năm trước
Cho nửa đường tròn tâm $O$ đường kính $AB.$ Vẽ các tiếp tuyến $Ax$ và $By$ ($Ax$ và $By$ và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là $AB$ ). Gọi $M$ là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại $M$ cắt $Ax$ và $By$ theo thứ tự tại $C$ và $D.$
Tìm vị trí điểm $M$ để tứ giác $ABDC$ có chu vi nhỏ nhất.
Trả lời bởi giáo viên
Đáp án đúng: c
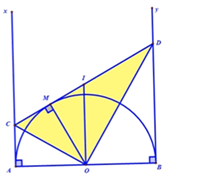
Xét tứ giác $ABDC$ có: $AC//BD \Rightarrow ABDC$ là hình thang
Vì hai tiếp tuyến \(CD\) và \(Ax\) cắt nhau tại \(C\), hai tiếp tuyến \(DC\) và \(By\) cắt nhau tại \(D\) nên \(AC = CM;BD = BM\) (tính chất hai tiếp tuyến cắt nhau).
Chu vi hình thang $ABDC$ là:
${C_{ABDC}} = AC + AB + BD + CD = CM + AB + DM + CD = AB + 2CD$ $ \Rightarrow {C_{ABDC}}_{\min }\,\,{\rm{khi}}\,\,\,C{D_{\min }} \Rightarrow CD = AB \Rightarrow CD//AB$
Mà $OM\; \bot CD \Rightarrow OM\; \bot AB$ $ \Rightarrow {C_{ABDC\min }} = AB + 2AB = 3AB$
Vậy chu vi nhỏ nhất của hình thang $ABDC$ là $3AB$ khi $OM\; \bot AB.$
Hướng dẫn giải:
Chỉ ra $ABDC$ là hình thang
Tính chu vi hình thang $ABDC$ rồi lập luận để có chu vi nhỏ nhất là \(CD//AB\) từ đó suy ra vị trí điểm \(M.\)
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
