Câu hỏi:
2 năm trước
Cho nửa đường tròn $\left( O \right)$ có đường kính $AB.$ Vẽ các tiếp tuyến $Ax,{\rm{ }}By$ ($Ax,{\rm{ }}By$ và nửa đường tròn cùng thuộc một nửa mặt phẳng có bờ là $AB$ ). Qua một điểm $M$ thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt $Ax$ và $By$ theo thứ tự ở $C$ và $D.$ Gọi $N = AD \cap BC,{\rm{ }}H = MN \cap AB.$ Chọn câu đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: a
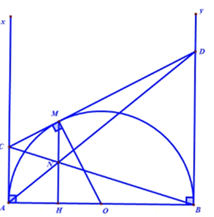
Theo tính chất hai tiếp tuyến cắt nhau ta có: $AC = CM$ và \(BD = DM\)
$AC//BD$ (vì cùng vuông góc với$AB$ )
Theo hệ quả của định lý Ta – lét ta có:
$\dfrac{{CN}}{{BN}} = \dfrac{{AC}}{{BD}} \Rightarrow \dfrac{{CN}}{{BN}} = \dfrac{{CM}}{{DM}}$
Theo định lý Ta – Lét đảo ta được $MN//BD.$
Mà $BD\; \bot AB \Rightarrow {\rm{ }}MN \bot \;AB$ nên A đúng
Theo hệ quả của định lý Ta – Lét ta có:
$\dfrac{{NH}}{{BD}} = \dfrac{{AH}}{{AB}} = \dfrac{{CN}}{{CB}} = \dfrac{{MN}}{{BD}} \Rightarrow MN = NH$ nên B sai.
Hướng dẫn giải:
+ Sử dụng tính chất hai tiếp tuyến cắt nhau và định lý Ta-lét
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
