Câu hỏi:
2 năm trước
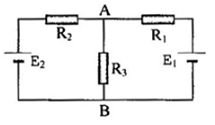
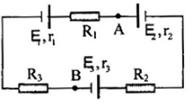
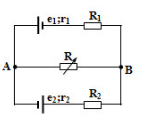
Cho mạch như hình vẽ:\({E_1} = 12V;{\rm{ }}{E_2} = 6V\); \({r_1} = {\rm{ }}{r_2} = 0,5\Omega \); \({R_1} = 4,5\Omega ;{R_2} = 2,5\Omega \). \(R\) là biến trở. Với giá trị nào của biến trở thì công suất trên \(R\)đạt cực đại, giá trị cực đại đó là?
Trả lời bởi giáo viên
Đáp án đúng: c
Ta xét nguồn tương đương gồm hai nhánh chứa hai nguồn \({E_1}\) và \({E_2}\)
Giả sử cực dương của nguồn tương đương ở A, chiều dòng điện như hình vẽ:
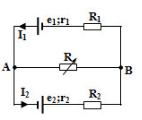
Biến trở \(R\) là mạch ngoài:
\(\begin{array}{l}\dfrac{1}{{{r_b}}} = \dfrac{1}{{{r_1} + {R_1}}} + \dfrac{1}{{{r_2} + {R_2}}} = \dfrac{1}{{0,5 + 4,5}} + \dfrac{1}{{0,5 + 2,5}} = \dfrac{8}{{15}}\\ \to {r_b} = \dfrac{{15}}{8}\Omega \end{array}\)
\({E_b} = \dfrac{{\dfrac{{{E_1}}}{{{r_1} + {R_1}}} - \dfrac{{{E_2}}}{{{r_2} + {R_2}}}}}{{\dfrac{1}{{{r_b}}}}} = \dfrac{{\dfrac{{12}}{{0,5 + 4,5}} - \dfrac{6}{{0,5 + 2,5}}}}{{\dfrac{8}{{15}}}} = \dfrac{3}{4}V = {U_{AB}}\)
Mạch tương đương:
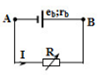
Để công suất trên R cực đại thì : \(R{\rm{ }} = {\rm{ }}{r_b} = \dfrac{{15}}{8}\Omega \)
\({P_{{\rm{max}}}} = \dfrac{{E_b^2}}{{4{{\rm{r}}_b}}} = \dfrac{{{{\left( {\dfrac{3}{4}} \right)}^2}}}{{4.\dfrac{{15}}{8}}} = \dfrac{3}{{40}}{\rm{W}}\)
Hướng dẫn giải:
Áp dụng định luật Ôm cho đoạn mạch
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
