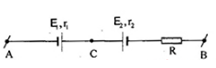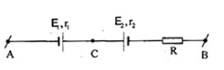
\({E_1} = 8V;{r_1} = 0,5\Omega \); \({E_2} = 2V;{r_2} = 0,4\Omega \);\(R = 15,1\Omega \); \({U_{AB}} = 6V\). Hiệu điện thế \({U_{AC}}\) và \({U_{CB}}\) là:
Trả lời bởi giáo viên
Giả sử dòng điện trong đoạn mạch có chiều từ A đến B.
Khi đó \({E_1}\) là máy phát, \({E_2}\) là máy thu.
+ Áp dụng định luật Ôm cho đoạn mạch AB, ta có: \(I = \dfrac{{{U_{AB}} + {E_1} - {E_2}}}{{R + {r_1} + {r_2}}} = \dfrac{{6 + 8 - 2}}{{15,1 + 0,5 + 0,4}} = \dfrac{3}{4}A\)
Nhận thấy \(I{\rm{ }} > {\rm{ }}0\) => điều giả sử là đúng hay dòng điện có chiều từ A đến B
+ Hiệu điện thế giữa hai điểm A và C: \({U_{AC}} = - {\rm{ }}{E_1} + {\rm{ }}I{r_1} = - 8{\rm{ }} + \dfrac{3}{4}.0,5 = - 7,625V\)
+ Hiệu điện thế giữa hai điểm C và B: \({U_{CB}} = {E_2} + {\rm{ }}I({r_2} + R) = 2 + \dfrac{3}{4}.(0,4 + 15,1) = 13,625V\)
Hướng dẫn giải:
+ Giả sử chiều dòng điện
+ Áp dụng định luật Ôm cho đoạn mạch