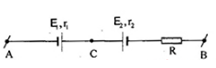
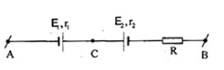
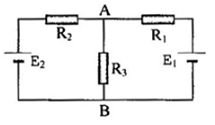
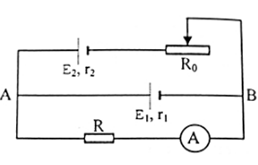
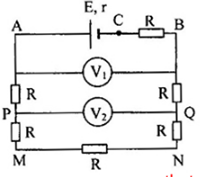
Cho mạch điện như hình vẽ:

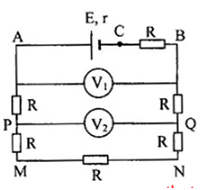
\(E = 12V\)

+ Khi \(r=0\) thì số chỉ vôn kế \(V_1\) là \(6V\)

+ Khi \({\rm{ }}r \ne 0\). Số chỉ trên \({V_1}\) là bao nhiêu? Biết mạch ngoài không đổi và công suất tiêu thụ ở mạch ngoài đạt cực đại. 

\({E_1} = 8V;{r_1} = 0,5\Omega \); \({E_2} = 2V;{r_2} = 0,4\Omega \);\(R = 15,1\Omega \); \({U_{AB}} = 6V\). Cường độ dòng điện trong mạch và chiều của nó là?

\({E_1} = 8V;{r_1} = 0,5\Omega \); \({E_2} = 2V;{r_2} = 0,4\Omega \);\(R = 15,1\Omega \); \({U_{AB}} = 6V\). Hiệu điện thế \({U_{AC}}\) và \({U_{CB}}\) là:

Cho mạch điện như hình vẽ:

\({E_1} = {\rm{ }}2,4V;{E_2} = {\rm{ }}3V\); \({r_1} = {\rm{ }}{r_2} = {\rm{ }}0\); \({R_1} = {\rm{ }}{R_3} = 15\Omega ;{R_2} = 10\Omega \). Cường độ dòng điện qua \({R_3}\) là:

Cho mạch điện như hình vẽ:

\(R = 8\Omega \);\({r_1} = {r_2} = 0,5\Omega \);\({R_A} = 0\). Khi dịch chuyển con chạy đến giá trị \({R_0}\) số chỉ của ampe kế không đổi bằng \(1A\) . Xác định \({E_1};{\rm{ }}{E_2} = ?\)

Cho mạch điện như hình vẽ:

\({E_1} = 6V\); \({r_1} = 0,6\Omega \); \({E_2} = 4V\); \({r_2} = 0,4\Omega \); \({E_3} = 14,6V;{r_3} = 0,6W\); \({R_1} = 6,4\Omega\); \({R_2} = 4\Omega\); \({R_3} = 6\Omega \). Hiệu điện thế \({U_{AB}}\) có giá trị là:

Cho mạch điện như hình vẽ:

\({E_1} = 1,9V;{r_1} = 0,3\Omega \); \({E_2} = 1,8V;{r_2} = 0,1\Omega \);\({E_3} = 1,6V;{r_3} = 0,1\Omega \). Ampe kế A chỉ số 0. Điện trở R có giá trị? Coi rằng điện trở của ampe kế không đáng kể, điện trở vôn kế vô cùng lớn.

Cho mạch điện như hình vẽ:

\(E = 12V\). Các vôn kế giống nhau, nếu \(r = 0\) thì số chỉ của vôn kế \(V_1\) là \(6V\) Số chỉ của vôn kế \({V_2}\) có giá trị là: