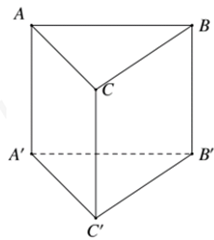
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A\), \(AB = a,AC = 2a\) và \(AA' = a\) (tham khảo hình vẽ bên). Tính khoảng cách \(d\) giữa hai đường thẳng \(AB'\) và \(A'C\).
Trả lời bởi giáo viên
Ta gắn hệ trục tọa độ \(Oxyz\) như hình vẽ. Coi \(a = 1\).
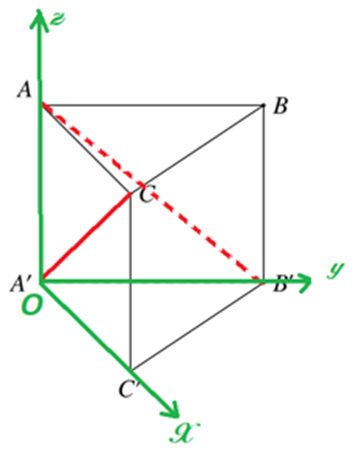
Ta có: \(A'\left( {0;0;0} \right)\), \(A\left( {0;0;1} \right)\), \(C'\left( {2;0;0} \right),\,\,B'\left( {0;1;0} \right)\), \(C\left( {2;0;1} \right)\).
Ta có: \(\overrightarrow {AB'} = \left( {0;1; - 1} \right),\,\,\overrightarrow {A'C} = \left( {2;0;1} \right),\,\,\overrightarrow {AA'} = \left( {0;0; - 1} \right)\).
\(\left[ {\overrightarrow {AB'} ,\overrightarrow {A'C} } \right] = \left( {1; - 2; - 2} \right)\) \( \Rightarrow \left[ {\overrightarrow {AB'} ,\overrightarrow {A'C} } \right].\overrightarrow {AA'} = 2\).
Vậy \(d\left( {AB',A'C} \right) = \dfrac{{\left| {\left[ {\overrightarrow {AB'} ,\overrightarrow {A'C} } \right].\overrightarrow {AA'} } \right|}}{{\left| {\left[ {\overrightarrow {AB'} ,\overrightarrow {A'C} } \right]} \right|}} = \dfrac{2}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 2} \right)}^2}} }} = \dfrac{2}{3}\) nên \(d = \dfrac{{2a}}{3}\).
Hướng dẫn giải:
- Sử dụng phương pháp tọa độ hóa. Đặt hệ trục tọa độ sao cho \(O \equiv A'\), C’, B’, A lần lượt nằm trên các tia Ox, Oy, Oz.
- Sử dụng công thức tính khoảng cách \(d\left( {AB',A'C} \right) = \dfrac{{\left| {\left[ {\overrightarrow {AB'} ,\overrightarrow {A'C} } \right].\overrightarrow {AA'} } \right|}}{{\left| {\left[ {\overrightarrow {AB'} ,\overrightarrow {A'C} } \right]} \right|}}\).


