Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là \({S_1}\) và \({S_2}\) (tham khảo hình vẽ).
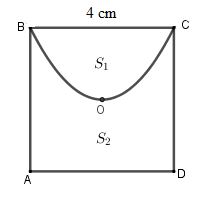
Tỉ số \(\dfrac{{{S_1}}}{{{S_2}}}\) bằng:
Trả lời bởi giáo viên
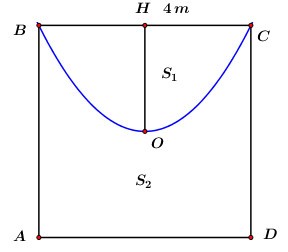
Gọi \(H\) là trung điểm của \(BC.\)
\(\begin{array}{l}{S_1} = \frac{4}{3}Rh = \frac{4}{3}.HC.OH = \frac{4}{3}.2.2 = \frac{{16}}{3}\,{m^2}.\\{S_{ABCD}} = {4^2} = 16\\ \Rightarrow {S_2} = {S_{ABCD}} - {S_1} = 16 - \frac{{16}}{3} = \frac{{32}}{3}\,\,{m^2}.\\ \Rightarrow \frac{{{S_1}}}{{{S_2}}} = \frac{{16}}{3}:\frac{{32}}{3} = \frac{1}{2}.\end{array}\)
Hướng dẫn giải:
Cách 1: Sử dụng ứng tích phân để tính diện tích hình phẳng.
Cách 2: Sử dụng công thức tính nhanh diện tích của parabol: \({S_1} = \frac{4}{3}Rh.\)
\({S_2} = {S_{ABCD}} - {S_1} \Rightarrow \frac{{{S_1}}}{{{S_2}}} = ...\)