Câu hỏi:
2 năm trước
Cho hình vuông ABCD cạnh a. Gọi M là trung điểm của AB. Hãy tính độ dài của vectơ →MD.
Trả lời bởi giáo viên
Đáp án đúng: c
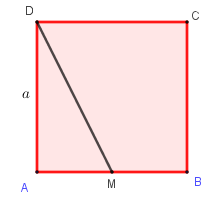
Áp dụng định lý Pitago trong tam giác vuông MAD ta có
DM2=AM2+AD2=(a2)2+a2=5a24⇒DM=a√52
Suy ra |→MD|=MD=a√52.
Hướng dẫn giải:
Tính độ dài đoạn thẳng MD, sử dụng định lý Pi-ta-go và kết luận đáp án đúng.

