Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Gọi \(M,N\) và \(E\) lần lượt là trung điểm của các cạnh \(AA',C'D'\) và \(CC'\) (tham khảo hình vẽ bên). Tính thể tích \(V\) của khối tứ diện \(BMNE\).
Trả lời bởi giáo viên
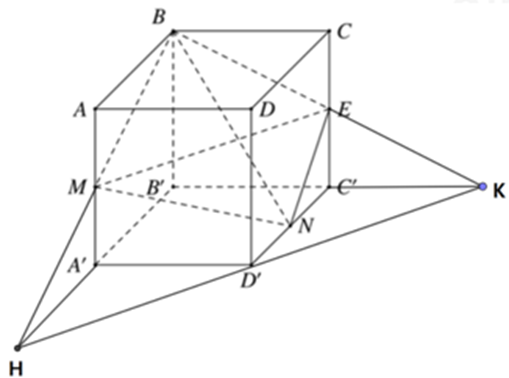
Trong mp\(\left( {ABB'A'} \right)\), gọi \(H = MB \cap A'B'\). Trong mp\(\left( {BCC'B'} \right)\), gọi \(K = BE \cap B'C'\).
Khi đó: \(\dfrac{{{V_{B.MNE}}}}{{{V_{B.HNK}}}} = \dfrac{{BM}}{{BH}}.\dfrac{{BE}}{{BK}} .\dfrac{{BN}}{{BN}}= \dfrac{1}{2}.\dfrac{1}{2}.1 = \dfrac{1}{4}\) \( \Rightarrow {V_{B.MNE}} = \dfrac{1}{4}{V_{B.HNK}}\).
Ta có: $A'H=A'B'=2ND'$
=> \(\left\{ \begin{array}{l}{S_{HNK}} = \dfrac{1}{2}{S_{A'HK}} = {S_{A'HD}} = \dfrac{1}{2}{a^2}\\d\left( {B;\left( {HNK} \right)} \right) = BB' = a\end{array} \right.\).
\( \Rightarrow {V_{B.HNK}} = \dfrac{1}{3}.\dfrac{1}{2}{a^2}.a = \dfrac{1}{6}{a^3}\)\( \Rightarrow {V_{B.MNE}} = \dfrac{1}{4}{V_{B.HNK}} = \dfrac{1}{{24}}{a^3}\).
Hướng dẫn giải:
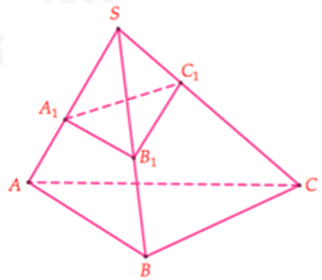
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác :
Cho khối chóp S.ABC, các điểm \({A_1},\,{B_1},\,{C_1}\) lần lượt thuộc \(SA,\,SB,\,SC\). Khi đó, \(\dfrac{{{V_{S.\,{A_1}{B_1}{C_1}}}}}{{{V_{S.ABC}}}} = \dfrac{{S{A_1}}}{{SA}}.\dfrac{{S{B_1}}}{{SB}}.\dfrac{{S{C_1}}}{{SC}}\).


