Câu hỏi:
2 năm trước
Cho hình lăng trụ tứ giác đều $ABCD.A'B'C'D'$ có cạnh đáy bằng $a$. Gọi $M$, $N$, $P$ lần lượt là trung điểm của $AB$, $BC$, $A'B'$. Tính khoảng cách giữa hai mặt phẳng $\left( {MNP} \right)$ và $\left( {ACC'} \right)$.
Trả lời bởi giáo viên
Đáp án đúng: d
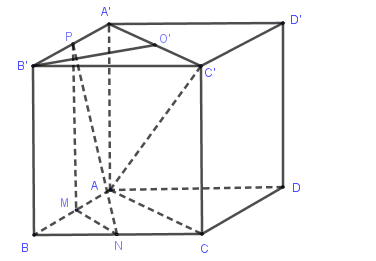
Ta có: $MM//AC,MP//A'A \Rightarrow \left( {MNP} \right)//\left( {ACC'} \right)$
$ \Rightarrow d\left( {\left( {MNP} \right);\left( {ACC'} \right)} \right) = d\left( {P;\left( {ACC'} \right)} \right) = \dfrac{1}{2}d\left( {B',\left( {ACC'} \right)} \right)$
Lại có:
\(B'O' \bot A'C',B'O' \bot CC' \Rightarrow B'O' \bot \left( {ACC'} \right)\) \( \Rightarrow d\left( {B',\left( {ACC'} \right)} \right) = B'O' = \dfrac{1}{2}B'D' = \dfrac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {P,\left( {ACC'} \right)} \right) = \dfrac{1}{2}d\left( {B',\left( {ACC'} \right)} \right) = \dfrac{{a\sqrt 2 }}{4}\)
Hướng dẫn giải:
- Chứng minh \(\left( {MNP} \right)//\left( {ACC'} \right) \Rightarrow d\left( {\left( {MNP} \right),\left( {ACC'} \right)} \right) = d\left( {P,\left( {ACC'} \right)} \right)\)
- Tính khoảng cách \(d\left( {P,\left( {ACC'} \right)} \right)\) bằng phương pháp tỉ lệ khoảng cách.
Câu hỏi khác
- Bài tập phần hai đường thẳng vuông góc thi ĐGTD Bách khoa
- Bài tập phần hai mặt phẳng vuông góc thi ĐGTD Bách khoa
- Bài tập phần góc giữa đường thẳng và mặt phẳng thi ĐGTD Bách khoa
- Bài tập phần đường thẳng vuông góc với mặt phẳng thi ĐGTD Bách khoa
- Bài tập góc giữa hai mặt phẳng môn toán ĐGNL có lời giải
