Câu hỏi:
2 năm trước
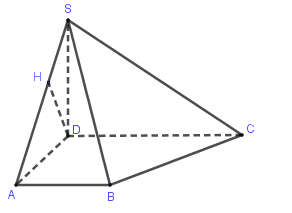
Cho hình thang vuông $ABCD$ vuông ở $A$ và $D$, $AD = 2a.$ Trên đường thẳng vuông góc với $\left( {ABCD} \right)$ tại $D$ lấy điểm $S$ với $SD = a\sqrt 2 .$ Tính khỏang cách giữa đường thẳng $DC$ và $\left( {SAB} \right)$.
Trả lời bởi giáo viên
Đáp án đúng: a
Vì $DC$// $AB$ nên $DC$// $\left( {SAB} \right)$
$ \Rightarrow d\left( {DC;\left( {SAB} \right)} \right) = d\left( {D;\left( {SAB} \right)} \right)$.
Kẻ $DH \bot SA$, do $AB \bot AD$, $AB \bot SD$ nên $AB \bot \left( {SAD} \right) \Rightarrow DH \bot AB$ suy ra $d\left( {D;\left( {SAB} \right)} \right) = DH$.
Trong tam giác vuông $SAD$ ta có:
$\begin{array}{l}
DH.SA = DS.DA\\
\Leftrightarrow DH = \frac{{DS.DA}}{{SA}} = \frac{{DS.DA}}{{\sqrt {S{D^2} + D{A^2}} }}\\
= \frac{{a\sqrt 2 .2a}}{{\sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {2a} \right)}^2}} }} = \frac{{2a\sqrt 3 }}{3} = \frac{{2a}}{{\sqrt 3 }}\\
\Rightarrow d\left( {DC,\left( {SAB} \right)} \right) = \frac{{2a}}{{\sqrt 3 }}
\end{array}$
Hướng dẫn giải:
Chứng minh \(CD//\left( {SAB} \right) \Rightarrow d\left( {CD,\left( {SAB} \right)} \right) = d\left( {D,\left( {SAB} \right)} \right)\)
Câu hỏi khác
- Bài tập phần hai đường thẳng vuông góc thi ĐGTD Bách khoa
- Bài tập phần hai mặt phẳng vuông góc thi ĐGTD Bách khoa
- Bài tập phần góc giữa đường thẳng và mặt phẳng thi ĐGTD Bách khoa
- Bài tập phần đường thẳng vuông góc với mặt phẳng thi ĐGTD Bách khoa
- Bài tập góc giữa hai mặt phẳng môn toán ĐGNL có lời giải
