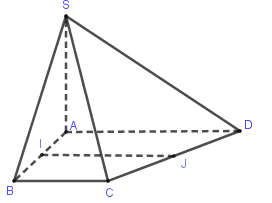
Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$, đáy $ABCD$ là hình thang vuông tại \(A,B\) có $AB = a$. Gọi $I$ và $J$ lần lượt là trung điểm của $AB$ và $CD$. Tính khoảng cách giữa đường thẳng $IJ$ và $\left( {SAD} \right)$. 

Cho hình thang vuông $ABCD$ vuông ở $A$ và $D$, $AD = 2a.$ Trên đường thẳng vuông góc với $\left( {ABCD} \right)$ tại $D$  lấy điểm $S$ với $SD = a\sqrt 2 .$ Tính khỏang cách giữa đường thẳng $DC$ và $\left( {SAB} \right)$.

Cho hình chóp $O.ABC$ có đường cao $OH = \dfrac{{2a}}{{\sqrt 3 }}$. Gọi $M$ và $N$ lần lượt là trung điểm của $OA$ và $OB.$ Khoảng cách giữa đường thẳng $MN$ và $\left( {ABC} \right)$ bằng:

Cho hình chóp tứ giác đều $S.ABCD$ có $AB = SA = 2a.$ Khoảng cách từ đường thẳng $AB$ đến $\left( {SCD} \right)$ bằng bao nhiêu?

Cho hình lăng trụ tứ giác đều $ABCD.A'B'C'D'$ có cạnh đáy bằng $a$. Gọi $M$, $N$, $P$ lần lượt là trung điểm của $AB$, $BC$, $A'B'$. Tính khoảng cách giữa hai mặt phẳng $\left( {MNP} \right)$ và $\left( {ACC'} \right)$.

Cho hình lăng trụ tam giác $ABC.A'B'C'$ có các cạnh bên hợp với đáy những góc bằng $60^\circ $, đáy $ABC$ là tam giác đều cạnh $a$ và $A'$ cách đều $A$, $B$, $C$. Tính khoảng cách giữa hai đáy của hình lăng trụ.

Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có cạnh bên bằng $a.$ Các cạnh bên của lăng trụ tạo với mặt đáy góc ${60^{\rm{o}}}.$ Hình chiếu vuông góc của $A'$ lên mặt phẳng $\left( {ABC} \right)$ là trung điểm của $BC$. Khoảng cách giữa hai mặt đáy của lăng trụ bằng bao nhiêu?