Câu hỏi:
2 năm trước
Cho hình chóp tứ giác đều $S.ABCD$ có $AB = SA = 2a.$ Khoảng cách từ đường thẳng $AB$ đến $\left( {SCD} \right)$ bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: b
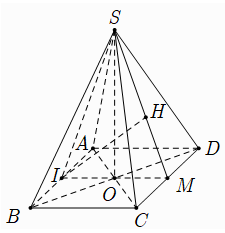
Gọi \(I,M\) lần lượt là trung điểm cạnh \(AB\) và \(CD\) thì \(\left\{ \begin{array}{l}CD \bot IM\\CD \bot SM\end{array} \right. \Rightarrow CD \bot (SIM)\)
Vẽ \(IH \bot SM\) tại \(H \in SM\)thì \(IH \bot (SCD)\)
Mà \(AB//CD \subset \left( {SCD} \right)\Rightarrow AB// (SCD)\)
\( \Rightarrow d\left( {AB,(SCD)} \right) = d\left( {I,(SCD)} \right) = IH = \dfrac{{SO.IM}}{{SM}}\)
\(\Delta SAB\) đều cạnh \(2a \Rightarrow SI = a\sqrt 3 \Rightarrow SM = a\sqrt 3 \)
Và \(OM = \dfrac{1}{2}IM = a \Rightarrow SO = \sqrt {S{M^2} - O{M^2}} = a\sqrt 2 \)
Cuối cùng \(d\left( {AB,(SCD)} \right) = \dfrac{{SO.IM}}{{SM}} = \dfrac{{a\sqrt 2 .2a}}{{a\sqrt 3 }} = \dfrac{{2a\sqrt 6 }}{3}\)
Hướng dẫn giải:
Gọi \(I,M\) là trung điểm của \(AB,CD\), kẻ \(IH \bot SM\) và chứng minh \(d\left( {AB,\left( {SCD} \right)} \right) = d\left( {I,\left( {SCD} \right)} \right) = IH\).
Câu hỏi khác
- Bài tập phần hai đường thẳng vuông góc thi ĐGTD Bách khoa
- Bài tập phần góc giữa đường thẳng và mặt phẳng thi ĐGTD Bách khoa
- Bài tập phần hai mặt phẳng vuông góc thi ĐGTD Bách khoa
- Bài tập phần đường thẳng vuông góc với mặt phẳng thi ĐGTD Bách khoa
- Bài tập góc giữa hai mặt phẳng môn toán ĐGNL có lời giải
