Cho hình chữ nhật $ABCD$ có \(AB = a;\,AD = b\) . Cho $M$ , $N$ , $P$ , $Q$ là các đỉnh của tứ giác $MNPQ$ và  lần lượt thuộc các cạnh $AB$ , $BC$ ,$CD,DA$ . Tìm giá trị nhỏ nhất của chu vi tứ giác $MNPQ$ .

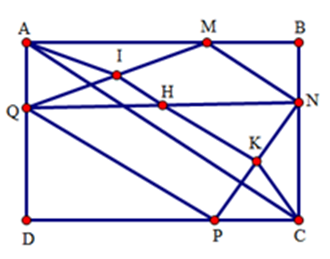
Gọi $I,H,K$ lần lượt là trung điểm các đoạn $QM,QN,PN$ .

Xét tam giác $AQM$ vuông tại $A$ có $AI$ là đường trung tuyến nên suy ra \(AI = \dfrac{1}{2}QM\).

$IH$ là đường trung bình của tam giác $QMN$ nên \(IH = \dfrac{1}{2}MN\), $IH$ //$MN$ .

Tương tự \(KC = \dfrac{1}{2}NP,HK = \dfrac{1}{2}PQ\), $HK$ //$PQ$ .

Do đó $AI{\rm{ }} + {\rm{ }}IH{\rm{ }} + {\rm{ }}HK{\rm{ }} + {\rm{ }}KC{\rm{ }} = \dfrac{1}{2}{P_{MNPQ}}$

Mặt khác nếu xét các điểm $A,I,H,K,C$ ta có: $AI{\rm{ }} + {\rm{ }}IH{\rm{ }} + {\rm{ }}HK{\rm{ }} + {\rm{ }}KC{\rm{ }} \ge AC$

Do đó \({P_{MNPQ}} \ge 2AC\) (không đổi)

Dấu “=” xảy ra khi và chỉ khi $A,I,H,K,C$ thẳng hàng theo thứ tự đó. Điều đó tương đương với

$MN$ //$AC$  //$QP$ , $QM$ //$BD$  //$NP$

hay $MNPQ$ là hình bình hành.

Theo định lý Pytago cho tam giác \(ACB\) vuông tại \(A\) ta có

\(A{C^2} = A{B^2} + B{C^2} = A{B^2} + A{D^2}\) \( = {a^2} + {b^2} \Rightarrow AC = \sqrt {{a^2} + {b^2}} \) .

Vậy giá trị nhỏ nhất của chu vi $MNPQ$ là $2AC$ \( = 2\sqrt {{a^2} + {b^2}} \) .