Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\)có đáy \(ABCD\) là hình thang \(\left( {AB//CD} \right)\). Gọi \(I,J\) lần lượt là trung điểm của các cạnh \(AD,\,BC\)và $G$ là trọng tâm tam giác \(SAB\). Biết thiết diện của hình chóp cắt bởi mặt phẳng \(\left( {IJG} \right)\) là hình bình hành. Hỏi khẳng định nào sao đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: c
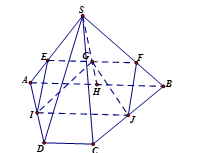
Vì \(\left( {IJG} \right) \cap \left( {SAB} \right) = \left\{ G \right\}\) ta có \(IJ//AB\) vì \(IJ\) là đường trung bình của hình thang \(ABCD\)
\(\left( {IJG} \right) \cap \left( {SAB} \right) = Gx//AB//IJ\). Gọi \(E = Gx \cap SA,F = Gx \cap SB\)
\(\left( {IJG} \right) \cap \left( {SAD} \right) = EI\);\(\left( {IJG} \right) \cap \left( {ABCD} \right) = IJ\);\(\left( {IJG} \right) \cap \left( {SBC} \right) = JF\)
Suy ra thiết diện \(\left( {IJG} \right)\) và hình chóp là hình bình hành $IJFE \Leftrightarrow IJ = EF\,\,\,\left( 1 \right)$
vì $G$ là trọng tâm tam giác $SAB \Leftrightarrow SG = \dfrac{2}{3}GH \Rightarrow EF = \dfrac{2}{3}AB\,\,\left( 2 \right)$
và \(IJ = \dfrac{{AB + CD}}{2}\,\,\,\,\left( 3 \right)\) vì\(IJ\)là đường trung bình của hình thang \(ABCD\)
Từ $\left( 1 \right)$,$\left( 2 \right)$ và$\left( 3 \right)$ $ \Rightarrow \dfrac{2}{3}AB = \dfrac{{AB + CD}}{2} \Leftrightarrow $ $4AB = 3AB + 3CD \Leftrightarrow AB = 3CD$
Hướng dẫn giải:
- Dựng thiết diện của hình chóp khi cắt bởi \(\left( {IJG} \right)\)
- Tìm điều kiện để thiết diện là hình bình hành và kết luận
